Cours & consultations astrologiques
![]() Astrologue atypique, concepteur d’Astrosoft et webmestre d’AstroAriana, Julien Rouger est aussi un scientifique, ingénieur généraliste, docteur en neurosciences et ingénieur-développeur informatique. Il vous propose ses consultations & cours conditionalistes.
Contactez-le sur son site personnel
Astrologue atypique, concepteur d’Astrosoft et webmestre d’AstroAriana, Julien Rouger est aussi un scientifique, ingénieur généraliste, docteur en neurosciences et ingénieur-développeur informatique. Il vous propose ses consultations & cours conditionalistes.
Contactez-le sur son site personnel
Lire la suite
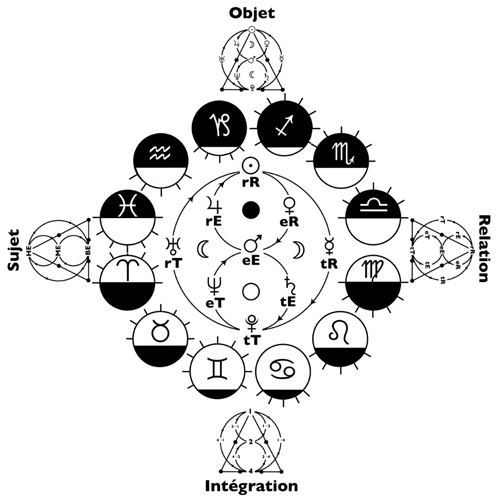
Représentation, Existence & Transcendance du Logoscope
![]() Dans cet ouvrage de maturité, Jean-Pierre Nicola revient sur les concepts clés qui ont permis de reconstruire l’astrologie sur des bases logiques, réalistes, naturelles et conditionnelles, en particulier le système R.E.T. (Représentation-Existence-Transcendance) et sa matrice, le Logoscope.
Alternant synthèses de vulgarisation et développements exigeants et audacieux, cet ouvrage permet différents (...)
Dans cet ouvrage de maturité, Jean-Pierre Nicola revient sur les concepts clés qui ont permis de reconstruire l’astrologie sur des bases logiques, réalistes, naturelles et conditionnelles, en particulier le système R.E.T. (Représentation-Existence-Transcendance) et sa matrice, le Logoscope.
Alternant synthèses de vulgarisation et développements exigeants et audacieux, cet ouvrage permet différents (...)
Lire la suite
Guide pratique d’astrologie moderne
![]() Ce Guide d’astrologie moderne est une réédition en 2022, sous un nouveau nom, du Guide d’astrologie conditionaliste paru en 1994. Les raisons de ce changement de nom sont expliquées dans l’article Astrologie moderne, naturelle ou conditionaliste ? (Fil d’Ariana n° 13, avril 2000). On remarquera que la réédition de La Condition solaire chez le même éditeur en 2022 avait été elle aussi l’occasion d’un (...)
Ce Guide d’astrologie moderne est une réédition en 2022, sous un nouveau nom, du Guide d’astrologie conditionaliste paru en 1994. Les raisons de ce changement de nom sont expliquées dans l’article Astrologie moderne, naturelle ou conditionaliste ? (Fil d’Ariana n° 13, avril 2000). On remarquera que la réédition de La Condition solaire chez le même éditeur en 2022 avait été elle aussi l’occasion d’un (...)
Lire la suite
Cycles planétaires, rétrogradations, zodiaque & constellations
![]() Ces dix vidéos représentent les cycles géocentriques du Soleil, de la Lune et des planètes. L’écliptique est le plan de l’orbite apparente du Soleil autour de la Terre. Les trajectoires de la Lune et des planètes s’effectuent sur des orbites plus ou moins inclinées sur le plan écliptique. Dans ce référentiel écliptique, une planète se caractérise ainsi par deux coordonnées : sa longitude écliptique (...)
Ces dix vidéos représentent les cycles géocentriques du Soleil, de la Lune et des planètes. L’écliptique est le plan de l’orbite apparente du Soleil autour de la Terre. Les trajectoires de la Lune et des planètes s’effectuent sur des orbites plus ou moins inclinées sur le plan écliptique. Dans ce référentiel écliptique, une planète se caractérise ainsi par deux coordonnées : sa longitude écliptique (...)
Lire la suite
Zodiaque des Signes & constellations : vidéos
![]() L’écliptique et les constellations
L’écliptique est la trajectoire apparente décrite chaque année par le Soleil autour de la Terre. Par définition, le Soleil se trouve toujours exactement sur l’écliptique. Toutefois le Soleil occupe différentes positions au nord ou au sud de l’équateur terrestre, en fonction du moment de l’année.
Les équinoxes correspondent au moment où le Soleil est dans le plan de (...)
L’écliptique et les constellations
L’écliptique est la trajectoire apparente décrite chaque année par le Soleil autour de la Terre. Par définition, le Soleil se trouve toujours exactement sur l’écliptique. Toutefois le Soleil occupe différentes positions au nord ou au sud de l’équateur terrestre, en fonction du moment de l’année.
Les équinoxes correspondent au moment où le Soleil est dans le plan de (...)
Lire la suite
Variations de l’arc diurne du Soleil au cours de l’année zodiacale : vidéo
![]() De l’équinoxe de mars au solstice de décembre
Équinoxe de mars
▶ le Soleil quitte le secteur écliptique des Poissons et entre dans celui du Bélier. Il se trouve alors à la verticale de l’équateur terrestre.
▶ partout sur Terre, le Soleil se lève à l’est et se couche à l’ouest, tandis que les durées des jours et des nuits sont pratiquement égales (12 heures chacune).
▶ dans tout l’hémisphère nord c’est (...)
De l’équinoxe de mars au solstice de décembre
Équinoxe de mars
▶ le Soleil quitte le secteur écliptique des Poissons et entre dans celui du Bélier. Il se trouve alors à la verticale de l’équateur terrestre.
▶ partout sur Terre, le Soleil se lève à l’est et se couche à l’ouest, tandis que les durées des jours et des nuits sont pratiquement égales (12 heures chacune).
▶ dans tout l’hémisphère nord c’est (...)
Lire la suite
Mort de Jean-Pierre Nicola
![]() Jean-Pierre Nicola est mort vendredi 21 octobre 2022 dans sa 93e année. Il fut sans doute le plus important astrologue du XXe siècle. Grâce à ses recherches et à ses découvertes, l’astrologie est devenue un authentique savoir contemporain. J’ai perdu un vieux compagnon.
Hommages à Jean-Pierre Nicola
Jean-Pierre Nicola, astrologue-découvreur
Témoignage astro de Jean-Pierre Nicola
La Condition (...)
Jean-Pierre Nicola est mort vendredi 21 octobre 2022 dans sa 93e année. Il fut sans doute le plus important astrologue du XXe siècle. Grâce à ses recherches et à ses découvertes, l’astrologie est devenue un authentique savoir contemporain. J’ai perdu un vieux compagnon.
Hommages à Jean-Pierre Nicola
Jean-Pierre Nicola, astrologue-découvreur
Témoignage astro de Jean-Pierre Nicola
La Condition (...)
Lire la suite
Petite histoire de La Condition solaire
![]() Dans le désert
Voici la petite histoire de La Condition solaire. J’ai commencé la rédaction de ce livre en octobre 1956, dans le Hoggar, en dehors des tâches professionnelles justifiées par une mission de 6 mois au titre d’agent technique dans une société de recherches minières. Au printemps 57, j’ai poursuivi ma rédaction sous les toits de Paris dans une chambre de bonne. En 1959, grâce aux relations (...)
Dans le désert
Voici la petite histoire de La Condition solaire. J’ai commencé la rédaction de ce livre en octobre 1956, dans le Hoggar, en dehors des tâches professionnelles justifiées par une mission de 6 mois au titre d’agent technique dans une société de recherches minières. Au printemps 57, j’ai poursuivi ma rédaction sous les toits de Paris dans une chambre de bonne. En 1959, grâce aux relations (...)
Lire la suite
20 personnalités et leurs Planètes dominantes
 Mini-portraits de personnalités abordés dans cette présentation :
▶ Dominante Soleil : Catherine Deneuve & Jean Dujardin
▶ Dominante Vénus : Gad Elmaleh & Marion Cotillard
▶ Dominante Mercure : Claire Chazal & Dany Boon
▶ Dominante Jupiter : Nicolas Bedos & Julie Depardieu
▶ Dominante Mars : Florence Foresti & Coluche
▶ Dominante Saturne : Sylvie Testud & Benoît (...)
Mini-portraits de personnalités abordés dans cette présentation :
▶ Dominante Soleil : Catherine Deneuve & Jean Dujardin
▶ Dominante Vénus : Gad Elmaleh & Marion Cotillard
▶ Dominante Mercure : Claire Chazal & Dany Boon
▶ Dominante Jupiter : Nicolas Bedos & Julie Depardieu
▶ Dominante Mars : Florence Foresti & Coluche
▶ Dominante Saturne : Sylvie Testud & Benoît (...)
Lire la suite
Les antisces et contre-antisces ne sont pas des Aspects
 Annexe
Nous avons observé que de nombreux astrologues du XVIIe siècle considéraient les parallèles de déclinaison ou antisces comme des Aspects. C’est une erreur qui s’est perpétuée et nous allons le démontrer. Et en passant, nous allons réhabiliter les perpendiculaires de déclinaisons ou contre-antisces, injustement négligés par la plupart des astrologues anciens ou contemporains.
La vidéo ci-dessous (...)
Annexe
Nous avons observé que de nombreux astrologues du XVIIe siècle considéraient les parallèles de déclinaison ou antisces comme des Aspects. C’est une erreur qui s’est perpétuée et nous allons le démontrer. Et en passant, nous allons réhabiliter les perpendiculaires de déclinaisons ou contre-antisces, injustement négligés par la plupart des astrologues anciens ou contemporains.
La vidéo ci-dessous (...)
Lire la suite
La théorie conditionaliste des Aspects
 Jean-Pierre Nicola et la première théorie des Aspects
C’est entre autre en retournant aux préoccupations et observations des premiers astronomes-astrologues mésopotamiens et en méditant sur l’échec de Kepler que, dans la seconde moitié du XXe siècle, l’astrologue Jean-Pierre Nicola (1929) a refondé la conception des Aspects, inchangée depuis Ptolémée voire Kepler, ce qui a constitué une véritable (...)
Jean-Pierre Nicola et la première théorie des Aspects
C’est entre autre en retournant aux préoccupations et observations des premiers astronomes-astrologues mésopotamiens et en méditant sur l’échec de Kepler que, dans la seconde moitié du XXe siècle, l’astrologue Jean-Pierre Nicola (1929) a refondé la conception des Aspects, inchangée depuis Ptolémée voire Kepler, ce qui a constitué une véritable (...)
Lire la suite
Les avancées au cours du XXe siècle
 La longue histoire de la conception des Aspects et de leurs orbes montre que pour les mesurer, la très grande majorité des astrologues savants, qui étaient en général aussi des astronomes, a pratiquement toujours négligé les latitudes écliptiques des planètes. L’absence de cette coordonnée dans le calcul des Aspects est un phénomène d’autant plus intéressant et significatif que ces observateurs et (...)
La longue histoire de la conception des Aspects et de leurs orbes montre que pour les mesurer, la très grande majorité des astrologues savants, qui étaient en général aussi des astronomes, a pratiquement toujours négligé les latitudes écliptiques des planètes. L’absence de cette coordonnée dans le calcul des Aspects est un phénomène d’autant plus intéressant et significatif que ces observateurs et (...)
Lire la suite
Les innovations des XIXe & XXe siècles
 La fin du XIXe et les toutes premières années du XXe siècle voient apparaître deux innovations majeures dans la conception et la perception des Aspects et de leurs orbes. On doit le renouveau conceptuel aux astrologues anglais Zadkiel et Alan Leo, et la rénovation graphique, donc perceptive, à l’astrologue français Paul Choisnard. Ils ne se connaissaient pas et ignoraient très probablement leurs (...)
La fin du XIXe et les toutes premières années du XXe siècle voient apparaître deux innovations majeures dans la conception et la perception des Aspects et de leurs orbes. On doit le renouveau conceptuel aux astrologues anglais Zadkiel et Alan Leo, et la rénovation graphique, donc perceptive, à l’astrologue français Paul Choisnard. Ils ne se connaissaient pas et ignoraient très probablement leurs (...)
Lire la suite
La conception des Aspects du XVIIe au XIXe siècle
 L’après-Kepler
Les Aspects planétaires sont donc désormais clairement identifiés comme tels par une minorité d’astrologues savants, et non comme des dépendances de la géométrie zodiacale ptoléméenne, même si cette dernière conserve une certaine influence sur leur définition et sur les orbes admis. Les débats théoriques à leur sujet porteront désormais beaucoup sur les orbes et un tout petit peu sur les (...)
L’après-Kepler
Les Aspects planétaires sont donc désormais clairement identifiés comme tels par une minorité d’astrologues savants, et non comme des dépendances de la géométrie zodiacale ptoléméenne, même si cette dernière conserve une certaine influence sur leur définition et sur les orbes admis. Les débats théoriques à leur sujet porteront désormais beaucoup sur les orbes et un tout petit peu sur les (...)
Lire la suite
La notion d’Aspect chez Kepler au XVIIe siècle
 L’astrologie en pleine ébullition
L’œuvre de l’astronome-astrologue allemand Johannes Kepler (1571–1630) se situe à un moment-clé de l’histoire des sciences, un siècle après la révolution copernicienne : avec Copernic (1473–1543), on est passé du géocentrisme à l’héliocentrisme et Kepler a découvert que les orbites planétaires n’étaient pas des cercles parfaits, mais des ellipses. Face à cette révolution dans (...)
L’astrologie en pleine ébullition
L’œuvre de l’astronome-astrologue allemand Johannes Kepler (1571–1630) se situe à un moment-clé de l’histoire des sciences, un siècle après la révolution copernicienne : avec Copernic (1473–1543), on est passé du géocentrisme à l’héliocentrisme et Kepler a découvert que les orbites planétaires n’étaient pas des cercles parfaits, mais des ellipses. Face à cette révolution dans (...)
Lire la suite
La notion d’Aspect du IIe siècle au XVIe siècle
 De la désuétude à la Renaissance
Deux-cents ans après Ptolémée, l’astrologie était progressivement tombée en désuétude dans l’Occident romano-chrétien, les astrologues européens sérieux et chercheurs se sont faits rarissimes entre le IVe et le XIIIe siècle, et n’ont guère laissé de traces. On se préoccupait désormais davantage du salut de son âme crucifiée que du statut des Aspects astrologiques. On ne sait (...)
De la désuétude à la Renaissance
Deux-cents ans après Ptolémée, l’astrologie était progressivement tombée en désuétude dans l’Occident romano-chrétien, les astrologues européens sérieux et chercheurs se sont faits rarissimes entre le IVe et le XIIIe siècle, et n’ont guère laissé de traces. On se préoccupait désormais davantage du salut de son âme crucifiée que du statut des Aspects astrologiques. On ne sait (...)
Lire la suite
Notion et concept d’Aspect planétaire
 Introduction
Les planètes sont le premier effecteur astrologique. L’Aspect est donc une entité astrologique essentielle, puisqu’il définit à la fois les fréquences-clés d’un cycle (Aspects d’une planète à elle-même au cours de sa période géocentrique) ou d’un intercycle (rapport privilégié qui s’établit périodiquement entre deux ou plusieurs planètes).
Dans les cartes du ciel contemporaines, les Aspects (...)
Introduction
Les planètes sont le premier effecteur astrologique. L’Aspect est donc une entité astrologique essentielle, puisqu’il définit à la fois les fréquences-clés d’un cycle (Aspects d’une planète à elle-même au cours de sa période géocentrique) ou d’un intercycle (rapport privilégié qui s’établit périodiquement entre deux ou plusieurs planètes).
Dans les cartes du ciel contemporaines, les Aspects (...)
Lire la suite
La notion d’Aspect chez Ptolémée au IIe siècle
 La notion originelle d’Aspect chez les Babyloniens
Aux débuts conjoints de l’astrologie et de l’astronomie il y a quelques millénaires, les savants-prêtres babyloniens ne prêtaient attention qu’à un seul Aspect : la conjonction (≈ 0°), phénomène céleste majeur parce que le plus visible. Les tablettes astronomico-astrologiques du XVIIIe au XVIe siècle AEC qui ont été retrouvées en attestent. Cet intérêt (...)
La notion originelle d’Aspect chez les Babyloniens
Aux débuts conjoints de l’astrologie et de l’astronomie il y a quelques millénaires, les savants-prêtres babyloniens ne prêtaient attention qu’à un seul Aspect : la conjonction (≈ 0°), phénomène céleste majeur parce que le plus visible. Les tablettes astronomico-astrologiques du XVIIIe au XVIe siècle AEC qui ont été retrouvées en attestent. Cet intérêt (...)
Lire la suite
Approche jungienne de l’astrologie
 Chercheur infatigable, Jean-Pierre Nicola apporte à l’astrologie depuis plus d’un demi-siècle, de par ses livres et nombreux articles, un décryptage rationnel liant astro-psychologie et astronomie. Monsieur Lee Gladden, Ph.D, Directeur de thèse, de l’université de Honolulu résume son apport :
“M. Nicola est une des rares personnes qui, dans son domaine de recherche, allie une pratique longue et (...)
Chercheur infatigable, Jean-Pierre Nicola apporte à l’astrologie depuis plus d’un demi-siècle, de par ses livres et nombreux articles, un décryptage rationnel liant astro-psychologie et astronomie. Monsieur Lee Gladden, Ph.D, Directeur de thèse, de l’université de Honolulu résume son apport :
“M. Nicola est une des rares personnes qui, dans son domaine de recherche, allie une pratique longue et (...)
Lire la suite
Astrologie et politique du mensonge
 D’un point de vue ontologique, les choses sont réelles ou non ; et d’un point de vue logique ou gnoséologique, les idées sont considérées comme vraies ou fausses selon qu’elles sont fondées sur des choses qui sont considérées comme réelles ou non. Car il faut le savoir : les définitions du réel et de l’irréel, du vrai et du faux varient selon les époques et les savoirs qui leurs sont associés. La réalité (...)
D’un point de vue ontologique, les choses sont réelles ou non ; et d’un point de vue logique ou gnoséologique, les idées sont considérées comme vraies ou fausses selon qu’elles sont fondées sur des choses qui sont considérées comme réelles ou non. Car il faut le savoir : les définitions du réel et de l’irréel, du vrai et du faux varient selon les époques et les savoirs qui leurs sont associés. La réalité (...)
Lire la suite
Tous droits réservés.
© 2003–2024
Richard Pellard. Reproduction interdite.
Webmestre :
Julien Rouger
AstroAriana — Site réalisé avec
SPIP