Organisation des demi-grands axes des orbites principales
Insatisfait autant de Titius, de Bode que de Schmidt, j’ai commencé en 1961 mes propres investigations sur les distances. Puisque les significations planétaires se déduisaient des intervalles de temps, j’ai supposé que les écarts de distances, selon le même principe plutôt que la même formule, devaient être révélatrices d’une structure ignorée. D’où la figure 2, construite à partir des différences successives des demi-grands axes.
| Planètes |
Dn |
− |
Dn − 1 |
= |
Différence |
| Pluton − Neptune |
39,6 |
− |
30,1 |
= |
9,5 |
| Neptune − Uranus |
30,1 |
− |
19,2 |
= |
10,9 |
| Uranus − Saturne |
19,2 |
− |
9,6 |
= |
9,5 |
| Saturne − Jupiter |
9,6 |
− |
5,2 |
= |
4,4 |
| Jupiter − Cérès |
5,2 |
− |
2,8 |
= |
2,4 |
| Cérès − Mars |
2,4 |
− |
1,5 |
= |
1,3 |
| Mars − Terre |
1,5 |
− |
1 |
= |
0,5 |
| Terre − Vénus |
1 |
− |
0,72 |
= |
0,28 |
| Vénus − Mercure |
0,72 |
− |
0,39 |
= |
0,33 |
| Mercure − Soleil |
0,39 |
− |
0 |
= |
0,39 |
Écarts en UA, valeurs arrondies des données de l’époque, sans différence avec celles du tableau I en dehors de Pluton. Une fois les interdistances reportées verticalement, en respectant horizontalement un écart systématique égal à l’unité, on peut tracer par les points obtenus deux cercles de rayons différents. Le plus petit n’aurait rien de singulier (par trois points non alignés on a toujours un cercle en géométrie euclidienne) si la projection des valeurs d’Uranus, Neptune, Pluton, sur le grand cercle n’acceptait pas, en abscisse, l’unité d’écart : 1.
Ces deux cercles méritaient un peu d’attention. Pourquoi l’unité, distance moyenne de la Terre au Soleil, et la Terre au point = 0, donnent-ils ce rayon apocalyptique ? Sans commenter les incidences ésotériques, parce qu’il y aurait trop à dire, j’ai proposé dans les Cahiers Astrologiques [1] une construction géométrique inédite du cercle 6,66 UA, et son satellite. Les enseignants du R.E.T. pourraient encore l’utiliser comme représentation des trois zones ‘R’, ‘E’, ‘T’ dans le système solaire, avec le ‘T’ concentré dans le petit cercle, le ‘E’ et le ‘R’ directement sur le grand, de part et d’autre de l’axe des abscisses.
L’information-symbole qui apparaît de cet essai est plus intéressante que l’information-signal. Malgré de meilleurs résultats, globalement, que ceux de la loi de Bode ou de Schmidt, je ne les ai pas trouvés suffisamment précis par rapport au moins de 1 % d’erreur que les mesures des distances laissent espérer. Mais si j’ai suivi une voie moins simple c’est après avoir dégagé de celle-ci des remarques profitables :
▶ a) Les points obtenus par les interdistances planétaires semblent dépendre d’un même rayon générateur, et former une courbe de la famille des coniques (cercle, ellipse, parabole, hyperbole).
▶ b) Le problème des distances moyennes change d’aspect si l’on adopte les coordonnées polaires. Il n’a jamais reçu de solution convaincante parce qu’il n’a pas été posé dans son plan réel : celui des fonctions périodiques, donc trigonométriques, associant angles et lignes dans nos systèmes de formalisation.
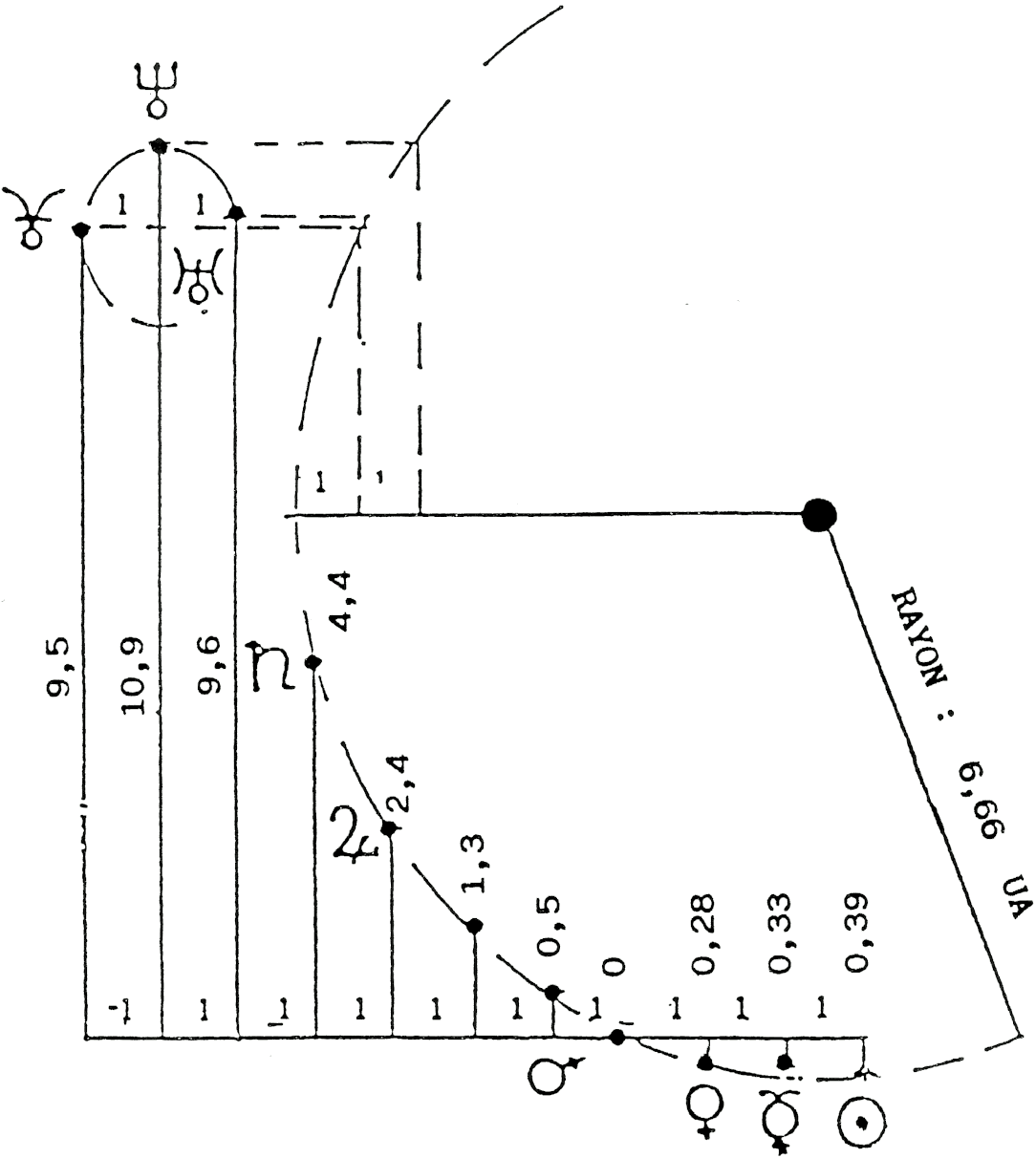
FIG. 2 — 6,66 : Le rayon de l’Apocalypse.
Ce schéma s’obtient par le report, verticalement, et à partir de Terre = 0, des écarts de distances d’une orbite à la suivante (unité UA). En attribuant le signe ‘−’ aux orbites intérieures (entre la Terre et le Soleil), le signe ‘+’ aux extérieures (au delà de la Terre), et un écart systématique de 1 sur l’axe des abscisses, il ressort de cet ensemble planétaire, traité géométriquement, un rayon de courbure variant autour de 1 / 6,66 avec une incertitude moyenne de 3 %.
1.4 — Progression par les angles
On pourrait croire que l’idée des intervalles est assez farfelue pour venir à l’esprit d’un astrologue. Pas du tout. Dans son livre, O. Schmidt rappelle la formule originale de l’astronome Gérard Pieter Kuiper pour retrouver les distances en fonction de M masse du Soleil, de m, masse des protoplanètes (planètes originelles), de Δ, distance entre les deux orbites, donc intervalle, et a, distance moyenne des protoplanètes au Soleil :

Mais pour que l’équation soit approximativement correcte, Kuiper doit supposer que la masse initiale de la protoplanète était des centaines de fois supérieure à la masse planétaire actuelle, ce qui ne séduit pas tellement O. Schmidt. Aucune perversité astrologique, on le voit, dans le traitement des distances par les intervalles ou par le rapport des masses que nous retrouverons en 2e partie… Ou alors, Kuiper est astrologisant ?
De tous les procédés que j’ai pu connaître, aucun n’utilise les angles. Pourtant, la pierre libérée d’une fronde en mouvement s’en échappe, normalement, par la tangente… Dans la figure 3, agrandissement d’un triangle de la figure 5, Mercure ne rejoint pas Vénus par un angle droit mais par un angle D̂ qui se déduit de l’angle Ĉ obtenu par le rapport des orbites, tel que :

Numériquement, pour cet exemple :
0,387 / 0,723 = 0,535 = sinus de l’angle 32,36°.
La surface (𝒮) d’un triangle est égale, en géométrie plane, à hauteur × base / 2. Dans la figure 3, la hauteur est une distance d et elle est égale à la base b. Pour chaque triangle où b désigne le demi-grand axe qui succède en ordre décroissant à l’orbite a la surface 𝒮 sera donc égale à b2 / 2.
Dans la conception newtonienne, la force de gravitation s’exprimant par une loi en 1 / R2, l’intensité d’action de la force centrale pourrait s’écrire : G ⋅ M / (2 ⋅ 𝒮)… au lieu de G ⋅ M / R2.
En supposant une force proportionnelle à l’aire du triangle b2 / 2, son produit avec l’intensité de la force centrale donnerait une constante, proportionnelle à la constante héliocentrique G ⋅ M.
Moment, du latin momentum qui signifie mouvement en est venu, en physique classique, à signifier instant. “Le temps étant toujours mesuré par un mouvement (celui des corps célestes, d’un pendule, etc.), un petit mouvement dans l’espace correspond à un petit moment — un instant — dans le temps.” [2]. Toujours en physique élémentaire, on appelle moment d’une force par rapport à un axe le produit de l’intensité de la Force (F vectoriel) par la distance entre sa droite d’action (support) et l’axe de rotation (Sz) perpendiculaire à cette droite. Comme le montre la fig. 4, ce moment peut être représenté par l’aire d’un triangle.
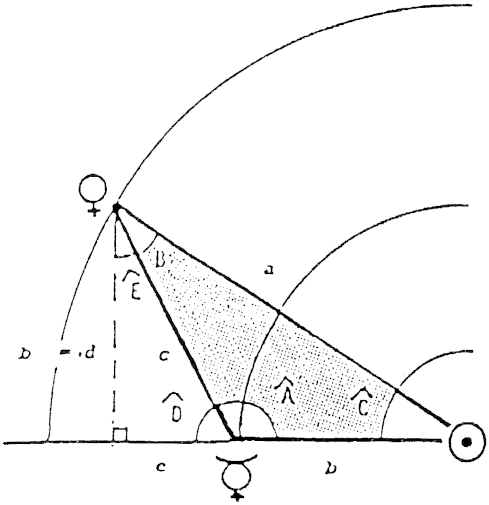
FIG. 3 — Détail de la progression des triangles formés par les demi-grands axes consécutifs.
On pose : sinus Ĉ = b / a avec b orbite inférieure succédant à l’orbite a. Ici :
- a = 0,723 (Vénus)
- b = 0,387 (Mercure)
- d = b
Cette particularité du triangle entraîne :

entre autres transformations.
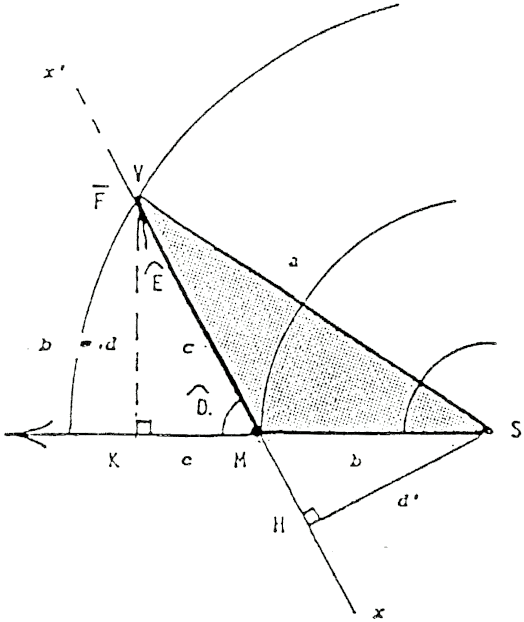
FIG. 4 — Représentation du moment d’une force par l’aire d’un triangle.
Supposons l’unité de force représentée par le vecteur MV = c = |F|.
Le moment de F par rapport a l’axe Sz, normal au plan de la figure, est, en valeur absolue égal au produit d′ par c. Soit :

Le produit SH ⋅ |F| = SH ⋅ MV représente deux fois l’aire du triangle SMV. L’aire de ce triangle se calcule également par le demi-produit de la base SM et de la hauteur VK. Donc :

VK étant égal à MV ⋅ sin D̂. L’expression devient :

Et pour le cas particulier où SM = VK = b :

Le produit |F| · d (grandeur de la force × distance ou bras de levier) mesure le pouvoir de rotation de la force. L’unité de moment est la combinaison de l’unité de la force et de l’unité de longueur, soit le newton-mètre. Les moments, grandeurs algébriques, permettent de définir des équilibres et des couples de forces.
Le système solaire est formé de couples planétaires. Faut-il expliquer son équilibre par les moments de ces couples ? Seule la progression proposée, en raison de son homogénéité avec la dimension en inverse carré de la loi de Newton, provoque ces questions et suggère de sonder, par-delà les moments, les structures-modèles de la matière et de son rayonnement. Commençons par la suite des triangles aux surfaces décroissantes, d’orbite en orbite, à partir de Pluton dont la distance moyenne au Soleil est prise pour origine (L0) des longitudes héliocentriques.
TABLEAU II — Rapports des demi-grands axes, conversions en angles et longitudes (Ln).
| Planète |
n |
Dn |
Rapports Dn / Dn - 1 |
arc sinus |
Sommation longitudes |
cot(Ln / 2) |
| Pluton |
0 |
39,438 7 |
|
|
0° L0 |
+∞ |
| Neptune |
1 |
30,109 6 |
0,763 5 a |
49°,77 Â |
49°,77 L1 |
2,155 8 |
| Uranus |
2 |
19,218 1 |
0,638 3 b |
39°,66 B̂ |
89°,43 L2 |
1,009 9 |
| Saturne |
3 |
9,554 7 |
0,497 2 c |
29°,81 Ĉ |
119°,24 L3 |
0,586 2 |
| Jupiter |
4 |
5,202 6 |
0,544 5 d |
32°,99 D̂ |
152°,23 L4 |
0,247 2 |
| Cérès |
5 |
2,77 |
0,531 9 e |
32°,14 Ê |
184°,37 L5 |
−0,038 2 |
| Mars |
6 |
1,523 7 |
0,550 6 f |
33°,41 F̂ |
217°,78 L6 |
−0,342 2 |
| Terre |
7 |
1 |
0,656 3 g |
41°,02 Ĝ |
258°,80 L7 |
−0,821 4 |
| Vénus |
8 |
0,723 3 |
0,723 3 h |
46°,33 Ĥ |
305°,13 L8 |
−1,926 3 |
| Mercure |
9 |
0,387 1 |
0,535 2 i |
32°,36 Î |
337°,49 L9 |
−5,025 |
|
|
0,148 2 |
0,382 8 j |
22°,51 Ĵ |
360° L0 |
−∞ |
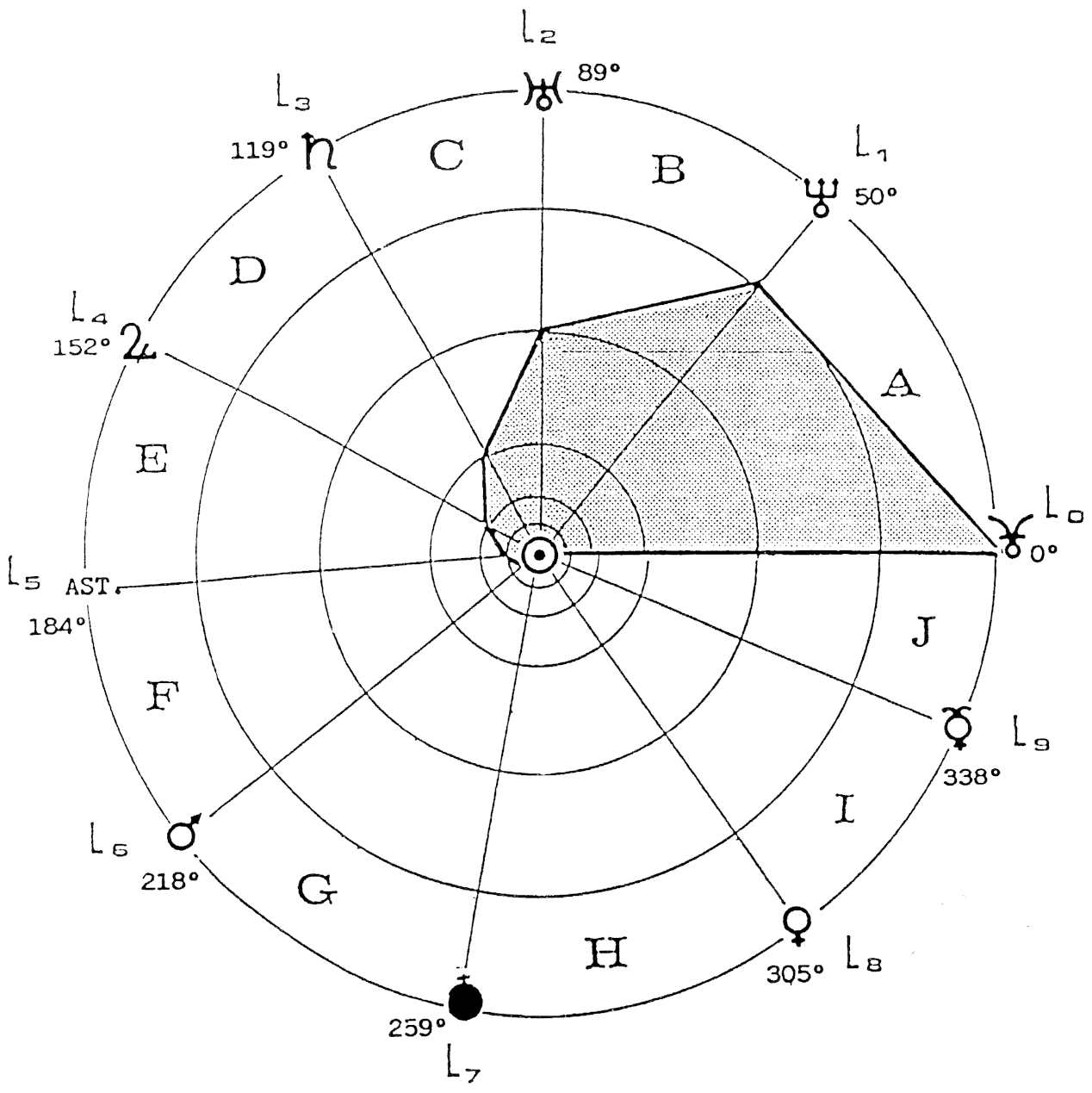
FIG. 5 — Graphe des longitudes obtenues par sommation des angles liés aux rapports des orbites consécutives (ordre de Pluton à Mercure).
Outre le mouvement différentiel des planètes, l’ensemble peut être en rotation, mais puisque les angles déterminent des constantes (les demi-grands axes des planètes), leurs directions dans l’espace pourraient être liées à un système invariant.
A priori, le rayon du cercle n’a pas de valeur absolue. On peut partir d’une valeur arbitraire pour exprimer les demi-grands axes en utilisant les indices (sinus) a, b, c, d,… qui eux, ne varient pas.
Ainsi, si l’on pose 39,5 UA = 1 :
| Pluton |
|
|
|
|
= |
1 |
| Neptune |
= |
(a) |
= |
0,763 |
= |
0,763 |
| Uranus |
= |
(a ⋅ b) |
= |
0,763 × 0,638 |
= |
0,487 |
| Saturne |
= |
(a ⋅ b ⋅ c) |
= |
0,763 × 0,638 × 0,497 |
= |
0,242 |
| Jupiter |
= |
(a ⋅ b ⋅ c ⋅ d) |
= |
0,763 × 0,638 × 0,497 × 0,545 |
= |
0,132 |
jusqu’à Mercure ou au Soleil par multiplication successive des coefficients, le résultat correct sera égal pour chaque planète, au quotient du demi-grand axe de la planète d’orbite n par le demi-grand axe de Pluton.
Suivant ce procédé, avec une unité comprise entre 0,1482 et 39,5 UA les valeurs inférieures s’obtiennent par multiplication, les valeurs supérieures par division de l’unité choisie. En posant 2,76 UA = 1, les distances deviennent :
| Pluton |
= |
1 / (a ⋅ b ⋅ c ⋅ d ⋅ e) |
= |
14,31 |
| Neptune |
= |
1 / (b ⋅ c ⋅ d ⋅ e) |
= |
10,86 |
| Uranus |
= |
1 / (c ⋅ d ⋅ e) |
= |
6,96 |
| Saturne |
= |
1 / (d ⋅ e) |
= |
3,45 |
| Jupiter |
= |
1 / (e) |
= |
1,47 |
| Cérès |
= |
1 |
= |
1 |
| Mars |
= |
1 × (f) |
= |
0,550 |
| Terre |
= |
1 × (f ⋅ g) |
= |
0,362 |
| Vénus |
= |
1 × (f ⋅ g ⋅ h) |
= |
0,262 |
| Mercure |
= |
1 × (f ⋅ g ⋅ h ⋅ i) |
= |
0,140 |
| Distance J |
= |
1 × (f ⋅ g ⋅ h ⋅ i ⋅ j) |
= |
0,054 |
Ce tableau détaillé, inutile à ceux qui ont la pratique des proportions, répond à la critique d’un cercle qui aurait le rayon de la Terre. Il montre l’intérêt de prendre pour unité le demi-grand axe de la planète au centre du système. Dans un système de 9 orbites principales… Jupiter est tout désigné. Inversement : si Jupiter est au centre, ou il n’y a que 9 orbites principales, ou leur nombre ne peut croître que par multiples de 2.
Sur la Fig. 5 la précision de la symétrie des longitudes par rapport à celle de Jupiter se mesure en effectuant les moyennes arithmétiques des couples dont la somme des numéros d’ordre égale 8, double du rang de Jupiter, à partir de Pluton 0.
| Jupiter |
|
|
|
|
|
= |
152°,2 |
| ½ (astéroïdes |
+ |
Saturne) |
= |
(184°,4 + 119°,3) |
/ 2 |
= |
151°,9 |
| ½ (Terre |
+ |
Neptune) |
= |
(258°,8 + 49°,8) |
/ 2 |
= |
154°,3 |
| ½ (Mars |
+ |
Uranus) |
= |
(217°,8 + 89°,4) |
/ 2 |
= |
153°,6 |
| ½ (Vénus |
+ |
Pluton) |
= |
(305°,1 + 0° ) |
/ 2 |
= |
152°,6 |
La règle des numéros d’ordre exclut le rang 9 de Mercure sans partenaire connu. En observant que sa longitude (337,5°) se situe à +4,8° de l’opposition de Jupiter (152,2° + 180° = 332,2°), ce n’est pas la position de Jupiter qui détermine la symétrie géométrique mais l’axe Jupiter-Mercure.
En quittant les angles pour les distances au Soleil la constante jupitérienne réapparaît avec le produit des demi-grands axes des couples de rang n + n′ = 8. Ce qui entraîne des produits également voisins pour les durées de révolutions sidérales, les vitesses, angulaire et linéaire, les accélérations dues à la force centrale.
TABLEAU III — Couples planétaires (produits des distances, vitesses linéaires, périodes, forces centrales).
| Couple |
D × D′(UA2) |
Vm × V′m (km2/s2) |
Rs × R′s (année2) |
√(f × f′) |
| Vénus - Pluton |
28,53 |
166 |
152,58 |
0,00021 |
| Terre - Neptune |
30,11 |
161,68 |
164,77 |
0,00020 |
| Mars - Uranus |
29,28 |
163,95 |
157,87 |
0,00020 |
| Cérès - Saturne |
26,35 |
172,45 |
135,49 |
0,00022 |
| Jupiter - Jupiter |
27,04 |
170,50 |
140,67 |
0,00022 |
| Moyennes |
5,322 |
12,922 |
12,272 |
0,00021 |
II ne s’agit jamais que d’une fonction d’inverse (y = cte / x) représentable par une hyperbole quadrilatère avec 5,32 UA comme unité de distance, ou d’une suite d’ellipses définies par :
| demi-petit axe |
 |
| demi-grand axe |
 |
Toutes ces ellipses, avec Jupiter pour la moins excentrique, peuvent avoir le Soleil comme foyer ou centre commun. Leur demi-petit axe varie autour de la valeur moyenne de 5,32 UA. Par rapport à cette unité, en reprenant le beau langage d’Evry Schatzman, c’est-à-dire les racines des distances, les erreurs vont de 0,5 % (Vénus-Pluton) a 6 % (Terre-Neptune), sans recours à des coefficients différents.
TABLEAU IV — Moyennes géométriques. Constante b = 5,3 (Jupiter) des couples planétaires.
| Couple |
√(D |
× |
D′) |
= |
b |
b / 5,32 |
| Vénus - Pluton |
√(0,723 |
× |
39,44) |
= |
5,341 |
1,005 |
| Terre - Neptune |
√(1 |
× |
30,11) |
= |
5,487 |
1,032 |
| Mars - Uranus |
√(1,524 |
× |
19,22) |
= |
5,412 |
1,018 |
| Cérès - Saturne |
√(2,77 |
× |
9,55) |
= |
5,144 |
0,968 |
| Jupiter |
|
|
|
= |
5,202 |
0,978 |
|
5,316 |
× |
5 |
= |
26,58 |
|
Ce consensus jupitérien donnait à penser à l’astrologue Maurice Froger que Mercure réclamait un partenaire à 73 UA, en réponse à la demande de 0,387 par 73 = 5,322. Prévenu par les limites du cercle 6,66 (la circonférence égale 41,85… valeur proche de Pluton), autant que par l’instabilité des extrêmes, j’ai opté pour la fermeture du groupe planétaire, non pour celui de la spirale, qui garde ses lignes d’orientation. Motifs de fermeture : ni Mercure, ni Pluton, de rang 9 et 0 ne satisfont à la convention de la somme des rangs = 8. Il était facile d’en déduire qu’au-delà de Pluton ou en-deçà de Mercure, tout nouvel astre n’aurait pas les caractéristiques d’appartenance au groupe “Jovien-Solaire” qui semble nôtre.
Cette affirmation purement fondée sur des considérations géométriques remonte à la publication de Nombres et Formes du Cosmos [3]. Renouvelée, chaque fois que j’ai pu le faire [4], à une époque où l’audace passait par la quête de transplutoniennes, elle n’est plus en manque d’explication depuis l’hypothèse rapportée par Michel Blanc dans un ouvrage collectif sur le système solaire [5] :
“La géométrie des régions externes de l’héliosphère a peut-être l’allure représentée sur la figure (Fig. 6). Le plasma interstellaire vient buter à 20 km/s sur une discontinuité de contact qui délimite la frontière externe de l’héliosphère (à moins qu’il n’ait été décéIéré avant par un choc). À l’intérieur de l’héliosphère doit probablement exister un choc au travers duquel le vent solaire redevient subsonique avant d’être dévié vers la région de l’héliosphère située en aval par rapport à l’écoulement du gaz interstellaire (vent interstellaire). Les calculs d’équilibre de pression situent ce choc interne à environ 100 à 130 unités astronomiques du Soleil (de l’ordre de trois fois la distance du Soleil à Pluton).”
J’ai souligné cette dernière phrase révélatrice du secret de nos limites… dans les calculs d’équilibre !
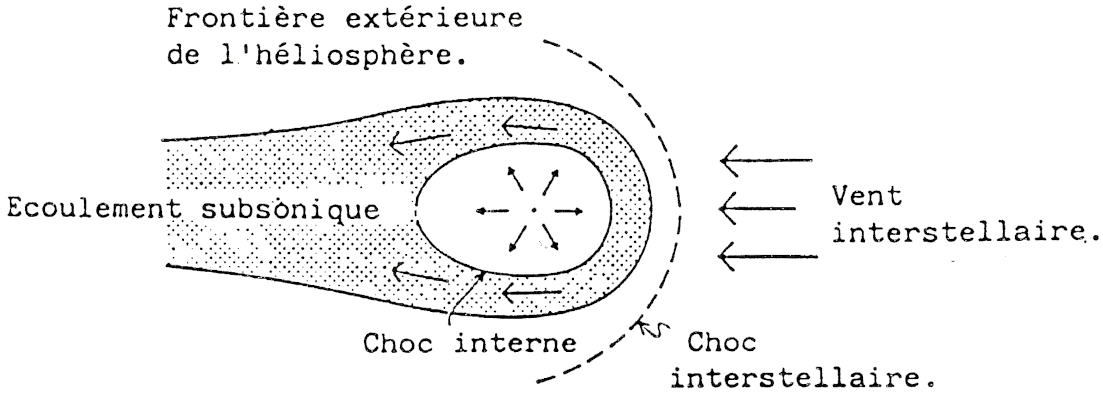
FIG. 6 — D’après W. I. Axford, “Interaction of the interstellar medium with the solar wind” (Space Science Reviews, 1973) le système solaire est pris dans une “bulle” coincé entre deux vents. Bien que les frontières fluctuent en raison de la variabilité du vent solaire et du milieu interstellaire, le principe de fermeture est scientifiquement admissible. Fallait-il être astrologue pour le déduire, en 1970, d’une simple figure géométrique ?
La famille planétaire constituée ne peut être perturbée par une transplutonienne inaugurant un improbable deuxième tour de spirale, forcément différent du premier. De plus, le coefficient qui boucle le cercle est égal à sinus 22,5° (0,382 7). Appliqué à Pluton (39,4) il nous vaudrait un astre à 39,4 / 0,3827 = 103 UA, distance désignée dans l’orbe des frontières de l’héliosphère. Appliqué à Mercure, la distance : 0,3827 × 0,3827 = 0,1481 UA… ne correspond pas au rayon du Soleil, même si à 0,169 UA, un corps céleste de masse négligeable aurait la période de révolution sidérale du Soleil, de 25,4 j à l’équateur [6]. Inutile de recourir aux racines, la distance 0,1481 UA sans planète permet d’exprimer les distances suivantes avec un chiffre voisin du 6,66 obtenu graphiquement. En effet : 0,1481 = 1 / 6,75. Avec les sinus des angles indiqués au tableau II :
| Mercure |
= |
1 / 6,75 × (sin Ĵ) |
= |
0,387 |
| Vénus |
= |
1 / 6,75 × (sin Ĵ ⋅ sin Î) |
= |
0,723 |
| Terre |
= |
1 / 6,75 × (sin Ĵ ⋅ sin Î ⋅ sin Ĥ) |
= |
1 |
| Mars |
= |
1 / 6,75 × (sin Ĵ ⋅ sin Î ⋅ sin Ĥ ⋅ sin Ĝ) |
= |
1,523 |
| Cérès |
= |
1 / 6,75 × (sin Ĵ ⋅ sin Î ⋅ sin Ĥ ⋅ sin Ĝ ⋅ sin F̂) |
= |
2,77 |
…et la suite par les sinus des angles F̂ à Â.
Le calcul des intervalles peut passer tout autant par la constante 6,75. Exemple, pour Cérès-Mars :
| Cérès-Mars |
 |
qui devient, après réduction et simplification :
| Cérès-Mars |
 |
| Constante |
 |
ou 1/0,148. Que l’on obtiendra de façon identique d’intervalle en intervalle.
Le traitement numérique des intervalles et sinus par les équations ci-dessus permet de chiffrer la valeur indicative autant que les insuffisances de la méthode graphique.

Article suivant — 1.4. Des cotangentes aux entiers simples
[1] Cahiers astrologiques nos 101 (1961), 108 (1964).
[2] Comprendre le langage des sciences. Isaac Asimov. Marabout Université, 1976.
[3] Nombres et formes du cosmos. Jean-Pierre Nicola. Éd. Traditionnelles, 1971.
[4] Peut-il exister une 10e planète ? Astrologique n° 15, 1978.
[5] Le système solaire, op. cit.
[6] Période de 33 j à 75° de latitude. Le Soleil est fluide, la durée de sa rotation apparente observable par les taches augmente de l’équateur aux pôles.