The cosmography is the description of the astronomical systems of the universe. In astrology, cosmography is limited to the description of the solar system and its main elements (Sun, Moon, Planets). The astrometry is the part of astronomy whose object is the measurement of the position of the stars and the determination of their movements (astronomy of position). It thus enters a part of astrometry into the cosmography of the solar system.
You will find a detailed presentation of the main physical characteristics of the Sun, the Moon and the Planets of the solar system in this section dedicated to them. Note that in astrology, we group under the term “Planets” (with a capital ‘P’) both the Sun, the Moon and the planets that revolve around the Sun. The use of this word with a capital letter does not mean that astrologers are unaware that the Sun and the Moon are not planets but respectively a star and the unique satellite of planet Earth.
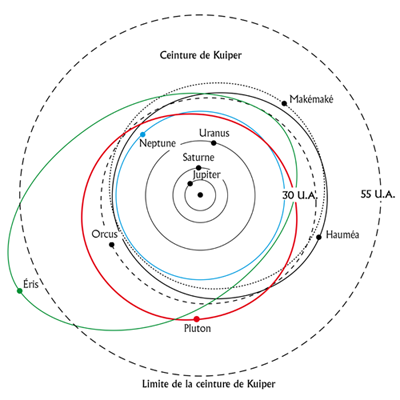
Let’s start with a broad view of our solar system. The diagram opposite represents the Sun (central point) and its planetary procession. Only the orbits of the slow planets are shown (from Jupiter) so as not to weigh down the representation. The orbits of Jupiter, Saturn, Uranus, Neptune and Pluto are therefore shown (in red), but also those of the small celestial bodies (some of which such as Hauméa, Makemake, Orcus or Eris have the rank of “dwarf planet” or are in the process of obtaining it) discovered at the edges of the solar system, inside the Kuiper belt, a ring of asteroids that surrounds the planetary system.
Pluto has meanwhile been officially relegated to the rank of “dwarf planet” (see it section devoted to this hysterical event). For astrologers, who don’t care about dictates grotesques of the International Astronomical Union, Pluto remains a short planet and the hypothetical influences of the dwarf planets are not taken into account for reasons which there is no need to develop here, but which can be briefly summarized: either they are small stars which are not plutinos and therefore do not have the same resonance as Pluto with Neptune like Hauméa and Makemake, either it is a plutino like the asteroid Orcus, a star whose physical characteristics mean that it has nothing to do with the planets “classics” like Eris.
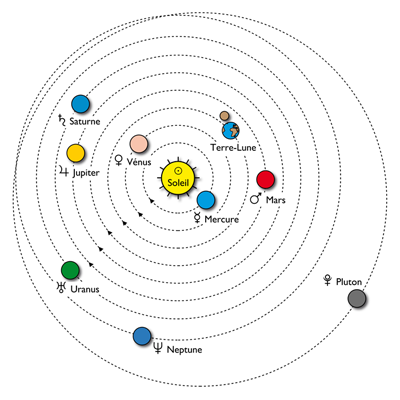
The planets that astrology takes into account are shown in the diagram opposite. In this purely symbolic representation, the orbital distances to the Sun are fictitious, the orbits are circular when in reality they are elliptical and the colors attributed to the planets are fanciful. The only small concession to realism, the orbit of Pluto intersects that of Neptune as in the real solar system.
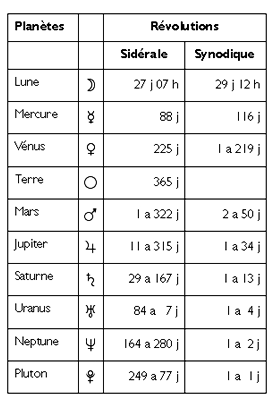
Astrology is based on a referential geocentric (= the Earth at the center), which does not mean that astrologers believe that it is located at the center of the universe and which does not exclude references heliocentric (= the Sun at the center of the solar system), especially when it comes to the durations of the sidereal revolutions of the planets, on which the Planetary Age Theory… and knowing that the synodic revolutions (geocentric) planets (time taken by a planet to return to the same Earth-planet-Sun configuration) are deduced by a simple formula from the durations of heliocentric orbital revolutions.
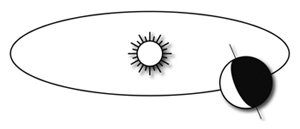
From a terrestrial observatory, therefore, it is the Sun, accompanied by its procession of planets, which seems to revolve around the Earth as in the diagram opposite which is only ever an illustration of change of repository compared to the previous one: from one to the other, we went from one heliocentric frame of reference (the Sun in the center) to a geocentric reference frame (the Earth in the center), without the reality having been betrayed, no offense to anti-astrologers.
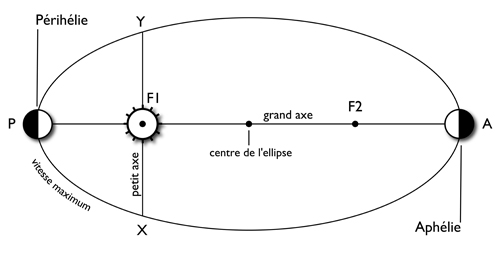The Sun is the star that occupies the center of the solar system. The planets describe around it almost circular elliptical orbits, of which the center of the Sun occupies one of the foci. The ellipses described by the planetary orbits mostly have a low eccentricity, except for that of Pluto, which is larger and causes it to cross the orbit of Neptune.
For all these orbits, the aphelion is the extremity of the major axis of the ellipse farthest from the Sun (and the planet is then the slowest in its orbit) and the perihelion closest (and the planet is then the fastest). In the diagram opposite, the eccentricity of the elliptical orbit and therefore the distance between the two foci F1 and F2 of the ellipse have been very clearly exaggerated for the clarity of the demonstration. In geocentric coordinates, the apogee means the orbital position of a planet or the Moon farthest from Earth and the perigee the closest.
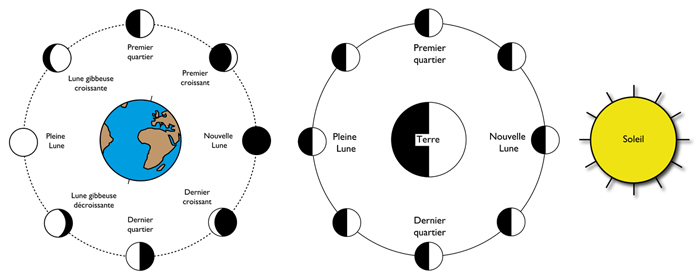
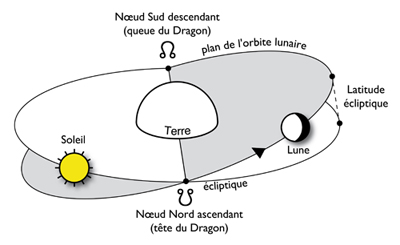All planetary orbits move in the plane of ecliptic, which is the apparent path of the Sun around the Earth, so named because this is where eclipses occur, which are either lunar (total or partial occultation of the Moon by the Sun), or solar (total or partial occultation of the Sun by the Moon).
To understand the phenomenon of eclipses, it is necessary to know that the plane of the lunar orbit is inclined to that of the solar orbit (the ecliptic), which it crosses at two points called knots: the ascending North node or dragon’s head and the descending South node or dragon’s tail (see diagram opposite). Eclipses occur when the Sun and Moon are at one of these points. Since the Sun and Moon have nearly identical apparent diameters, these eclipses can be total when the respective centers of the two stars are located exactly on one of the nodes or partial when this is not the case.
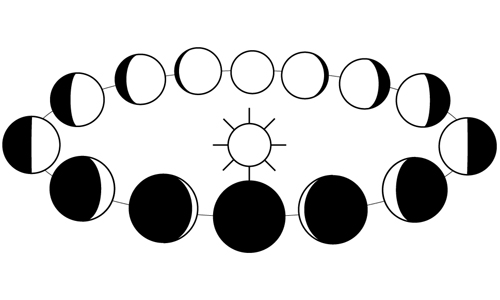
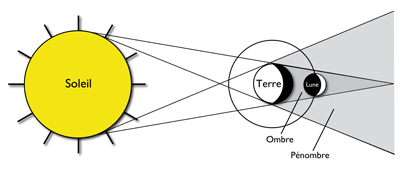Lunar eclipse: it occurs at the time of the full Moon (that is to say when the Earth is between the Sun and the Moon), when the Moon is near one of its nodes. The shadow of the Earth is then projected on the Moon, producing its temporary occultation. This concealment is said total if the Moon is exactly in the cone of shadow cast by the Earth, penumbral if it only crosses the penumbra zone, and partial when only part of the Moon enters the shadow.
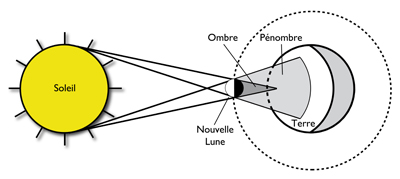Solar eclipse: it occurs at the time of the new Moon (i.e. when the Moon is between the Sun and the Earth). The solar eclipse is said total when the solar disk is completely occulted by that of the Moon, the solar corona remaining visible; she is said annular when the apparent size of the Moon is slightly smaller than that of the Sun; it is finally said partial when the Sun and the Moon are not perfectly aligned and the Moon only partially obscures the Sun.
All the planets travel their orbits in the direct direction (counter-clockwise), which is also the direction of their auto-rotation.
▶ The sidereal revolution is the time interval taken by a planet to complete a complete revolution around its center of attraction (the Earth for the Moon, the Sun for the planets).
▶ The synodic revolution is the time interval which separates two identical relative positions of a planet with respect to the Earth and the Sun (for example, conjunction of a planet with the Sun observed from the Earth). Synodic revolutions (geocentric cycles) are obtained by addition or subtraction between the terrestrial frequency and that of a planet, according to the equation:
▶ 1/S = 1/T − 1/A
▶ S = synodic revolution,
▶ A = sidereal revolution of the Earth and
▶ T = sidereal revolution of a planet.
Thus the appearances of the earthling are not illusions: it is indeed the durations of sidereal revolution (heliocentric for the Sun, geocentric for the Moon) which determine the synodic cycles. The table opposite gives the respective durations of sidereal and synodic revolutions for each star in the solar system.
The planets are classified according to their particular situations with respect to the Earth and the Sun. We thus distinguish:
▶ The “inferior” planets: Mercury and Venus, so named because they lie between the Sun and the Earth’s orbit (also called “interior”);
▶ The “superior” planets: from Mars to Pluto included. Their orbits are located beyond the Earth’s orbit (also called “outer”).
The characteristic phases of the apparent movements of the planets are conjunction, opposition, quadrature, sextile, trine and digression.
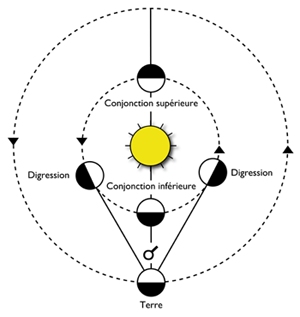Mercury and Venus, close to the Sun, never seem to move very far from it, seen from the terrestrial observatory. Their characteristic phases are the conjunction (lower or higher) and digression.
▶ Lower conjunction: Occurs when the planet is located between the Earth and the Sun on the Sun/Earth axis. Equivalent to the conjunction of the outer planets. It is during the inferior conjunction that the retrogradation of the inner planets occurs.
▶ Superior conjunction: Occurs when the planet is beyond (behind) the Sun on the same Sun/Earth axis. Equivalent to the opposition of the outer planets.
▶ Digression: the elongation of a planet being the angle of the directions of the Sun and the planet (360° for the outer planets), the digression is the maximum elongation of the inner planets (28° for Mercury and 46° for Venus, or for the latter the value of a half-square).
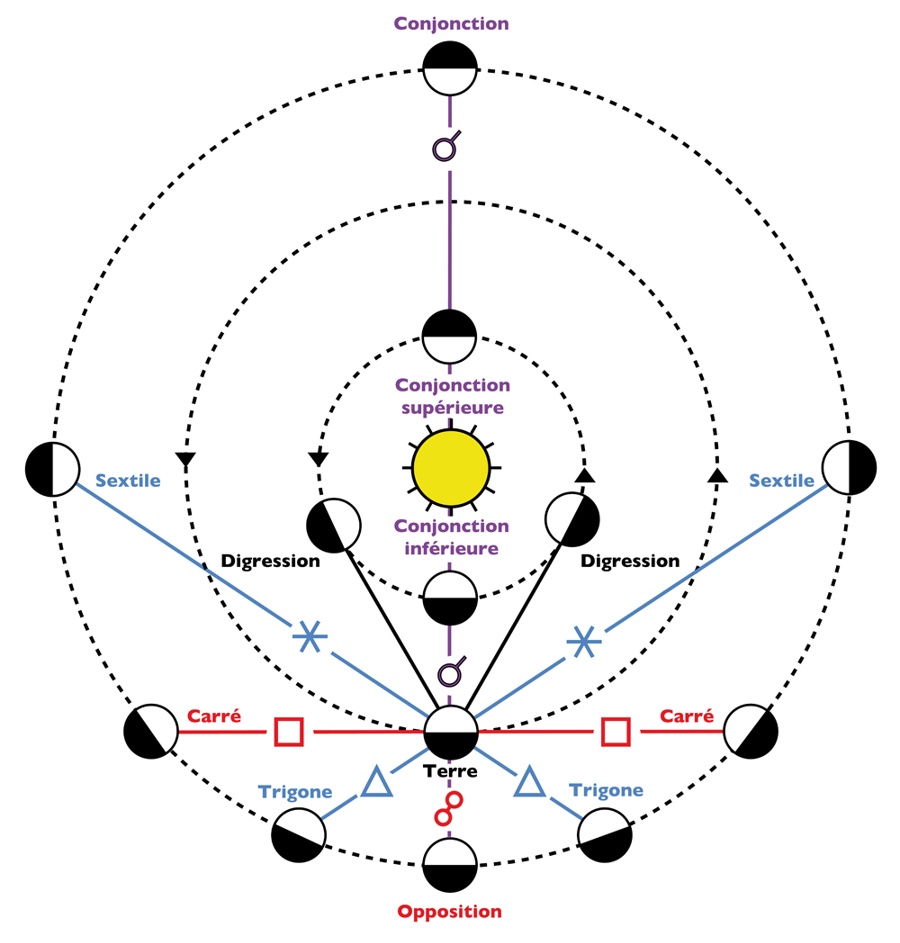The main angles or aspects formed by the outer planets are conjunction (0°), opposition (180°), square (90°), trine (120°) and sextile (60°).
When two planets are in the same direction with respect to the Earth, they are in conjunction (0° angle tolerating an orb of up to 18°);
When the Earth is located between two stars on the same axis, they are in opposition (180° angle tolerating an orb of up to 18°);
When the Sun-Earth-Planet angle is right, the planet is said to be in quadrature or square (90° angle tolerating an orb of up to 9°);
When the Sun-Earth-Planet angle is 120°, the planet is said to be in trine (angle tolerating an orb of up to 9°);
When the Sun-Earth-Planet angle is 60°, the planet is said to be in sextile (angle tolerating an orb of up to 5°);
The same angular deviations or Aspects can exist between the inner and outer planets, regardless of the Sun and its position.
The apparent (and not illusory) motion of a planet results from the composition of its real motion and that of the Earth. The figure below illustrates the retrogradation phenomenon of an outer planet, Mars. The inner planets, Mercury and Venus, also retrograde, according to specific modalities due to their particular astronomical situation. There retrogradation is characterized by three phases and five stations, in the direct direction, represented in the graph by five points on each orbit and on the sinusoid representing the apparent movements:
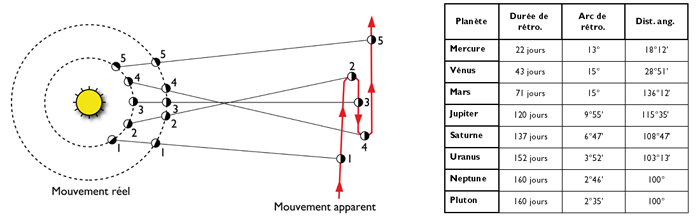
• Phase 1: direct sense, the perceived appearance accurately reflects the reality of the movement of Mars.
• Station 2: Mars seems “stop”. Symbol ‘R’ (for retrogradation) in the ephemeris, following the planetary position in degrees and minutes.
• Phase 3: Mars retrogrades and therefore appears to be moving in the opposite direction to its actual motion.
• Station 4: Mars seems again “stop”. Symbol “D” (for direct) in the ephemerides.
• Phase 5: Mars goes straight again.
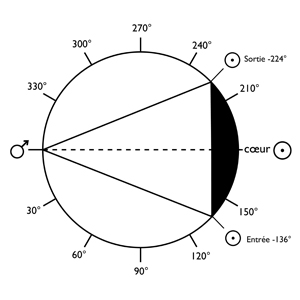
The cycle of retrogradations follows that of synodic revolutions. The table above illustrates the main characteristics, calculated as average values. The arc of retrogradation indicates the maximum orb of retrogradation (e.g. Mercury never moves more than 13° from the Sun on average during its retrogradation).
The angular distance indicates the number of degrees separating the planet from the Sun when the retrogradation begins (example: Mars goes into retrogradation when the Sun is at 136° “before” this planet, following the meaning of the signs; the retrogradation ends when the Sun is at −224° from the position of Mars at the start of the retrogradation).
At the heart of a retrogradation, the planet is in opposition to the Sun if it is an outer planet, in inferior conjunction if it is an inner planet. The characteristic effect of retrogradation is essentially to keep the planet retrograde for a fairly long time in a certain area of the ecliptic. Here again, the duration factor comes into play: the longer and longer a stimulus lasts, the more effective it is.
The Earth is a spheroid that can be divided into two equal hemispheres, separated by the equatorial plane: in the North, the Northern hemisphere and, in the South, the Southern hemisphere. The Earth revolves around itself from West to East, around a fixed axis passing through the North and South poles. The polar axis is, by definition, perpendicular to the equatorial plane. Earth’s rotation serves as a natural frame of reference for different coordinate systems.
Longitude and latitude
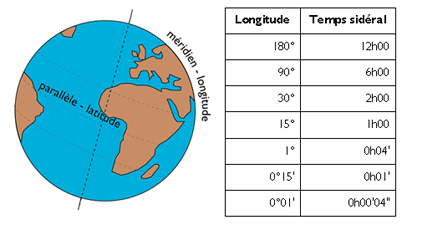Length: The large circles traced imaginarily on the surface of the Earth and passing through the poles are the meridians. By convention, it is assumed that there is one meridian per degree (i.e. 360 meridians), starting from the reference meridian, currently located vertically to the astronomical observatory of Greenwich (GB). From the meridian of Greenwich, we count the longitudes from 0° to + 180° going towards the East and from 0° to −180° going towards the West.
The Earth rotating around its axis in about 24 hours, we can express the terrestrial longitudes in sidereal time (time that measures the time it takes for any place on the earth’s surface to find itself in the same position vis-à-vis a so-called star “fixed”). Sidereal time is counted from 0h to +12 h 00 for East longitudes, and from 0h to −12 h 00 for West longitudes. It therefore takes an average of 4 minutes of sidereal time to cover one degree of longitude (rounded value, since the duration of terrestrial self-gyration is in fact 23 h 56 m).
Latitude: The great circles of position drawn on the Earth’s surface which are perpendicular to the meridians and parallel to the equator are called parallels. The parallels tell us the latitude North (from 0° to +90° from the equator) or South (from 0° to −90°) of a place, i.e. its distance from the equator.
It is a fixed and abstract sphere, of indeterminate radius, whose center is the eye of the terrestrial observer. Its two main coordinates are horizontal and the vertical.
▶ The vertical: it is the direction of a stationary plumb line. The vertical of a place passes through the zenith (highest point of the local sphere) and by the nadir (lowest point). All the imaginary circles passing through this axis are called vertical. The meridian of the place is called first vertical (nothing to do with the one in Greenwich, except in Greenwich).
▶ The horizontal: perpendicular to the vertical, therefore to the zenith-nadir axis. It’s the horizon, quite simply.
▶ The height of a star designates the angle formed by a star on its vertical with the horizontal plane; the zenith distance measures the angle formed by a star on its Vertical with the Zenith; height + zenith distance are therefore always equal to 90°. There are as many height circles than stars in the local sphere. The height circle, which passing through the center of the star, is parallel to the horizontal plane, is called almicantarat.
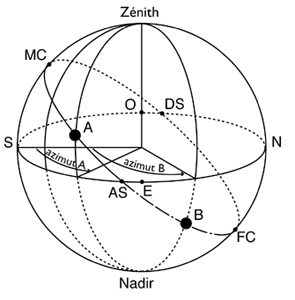- The azimuth of a star measures the angle formed by the vertical of the star and by the vertical of a terrestrial landmark designating the direction of the South. Conventionally, it is counted from 0° to 360° from left to right, i.e. in the direction of the diurnal movement, looking in the direction of the South for an observer located in the northern hemisphere. The diurnal movement is the course of a star above and below the horizon in 24 h 00, also called nychthemeron. Given the composition of the movement of the Earth with that of the stars in the local sphere, these seem to move in the opposite direction to their real movement. The nychthemeron is divided into two distinct periods: the diurnal arc (time of presence of a star above the horizontal plane) and the night bow (presence time below the horizontal plane). For the Sun and for him alone, the diurnal arc is synonymous with day and the nocturnal arc with night. The other celestial bodies can complete their diurnal arc at night, and their nocturnal arc during the day. Finally, it is on the horizontal plane that the four cardinal points (North, South, East, West) are projected into space.
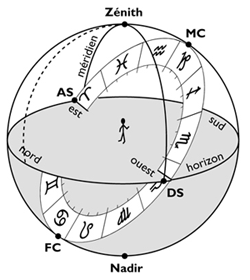
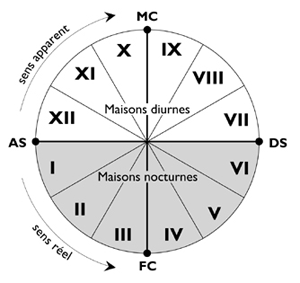The figure opposite represents the local sphere, which is divided into two hemispheres, the diurnal and the nocturnal, themselves divided into twelve sectors called Houses. We distinguish the real meaning of rotation of the Sun, the Moon and the Planets (opposite to that of a watch) and their apparent direction due to the rotation of the Earth. Traditionally, Houses are numbered in the real sense. To learn more about the Houses and the different sectors of the local sphere, refer to this section.
It is a fixed and abstract sphere, of indeterminate radius, whose center is this time the center of the Earth. The axis of the terrestrial poles, extending to infinity, becomes the axis of the world and the Earth’s equator is transformed in the same way into celestial equator.
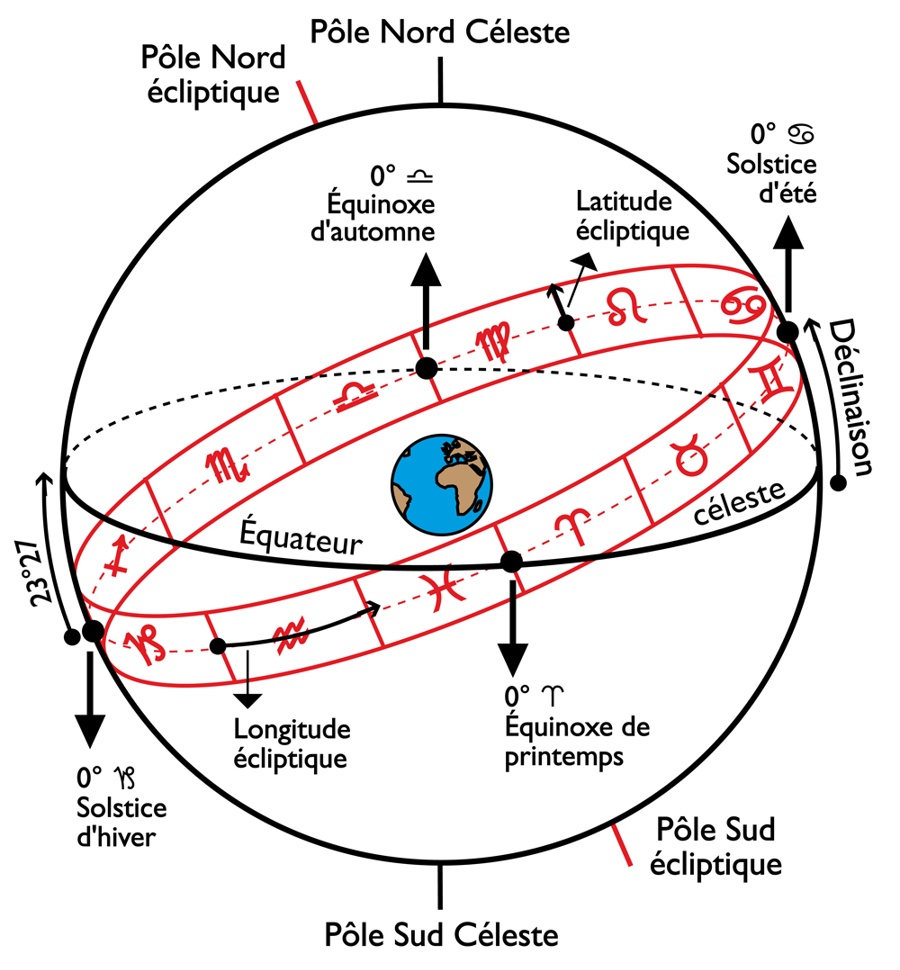
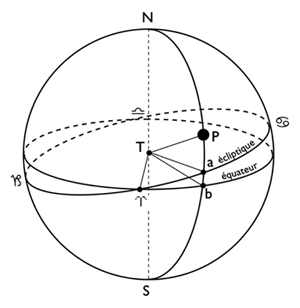In the geocentric frame of reference, the stars of the solar system traverse their apparent orbits in a plane called the ecliptic, so named because it is when the Sun and the Moon are on this plane that the solar or lunar eclipses (see below the phenomenon of eclipses). The axis of rotation of the Earth is tilted (skew of the axis) of 23.44° with respect to the plane of the ecliptic. Therefore, the equatorial plane and the ecliptic plane do not coincide. The diagram opposite shows the celestial sphere, whose center is the center of the Earth (‘T’).
The plane of the ecliptic is inclined with respect to that of the celestial equator (which is nothing other than the infinite extension of the earth’s equator), which it intersects at two points corresponding to the axis of the equinoxes (0° Aries–0° Libra), thus named because it is when the Sun passes over one of these points that the days and the nights are equal in duration. The axis of the solstices (not shown here) connects 0° Cancer (to the North) to 0° Capricorn (to the South); when the Sun passes through one of these two points, the diurnal and nocturnal durations reach their maximum inequalities according to the terrestrial latitudes. The Aries-T-b angle represents the right ascension of a planet, measured on the equator; the Aries-T-a angle represents the ecliptic longitude of a planet; finally, the planetary orbits being all more or less inclined on the plane of the ecliptic, the Aries-T-P angle represents the ecliptic latitude of a planet, i.e. its North or South height, positive or negative, with respect to this reference plane.
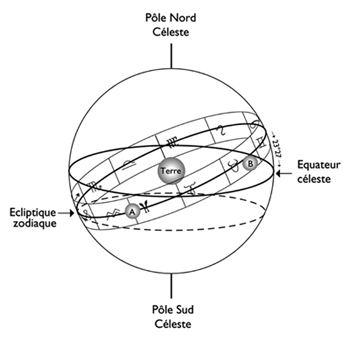This inclination of the orbits on the ecliptic plane gave rise to the zodiacal band. Its extent of 8° 30′ on either side of this plane was supposed to contain all planetary positions, including those of the planets with the strongest ecliptic latitudes (therefore the highest and the lowest with respect to the mean plane of the ecliptic). The zodiacal band therefore has no physical existence and it has no measurable radius: it is an abstract astronomical frame of reference for situating the planets in relation to the Earth. The extent of this zodiacal band has also ceased to be relevant since the discovery of Pluto, whose inclination of the orbit on the ecliptic (17° 32′) greatly exceeds the extent of the band. ecliptic. The figure opposite again represents the celestial sphere, this time with the zodiacal band in gray, on either side of the ecliptic. Points A and B represent two planetary positions: in A, the ecliptic latitude is zero and in B, it is maximum in the South. Position B therefore cannot be that of Pluto at its maximum ecliptic latitude, which is well below B.
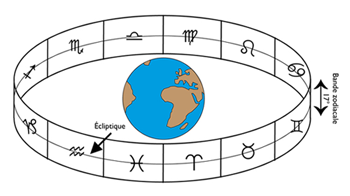The figure opposite represents the zodiacal band 17° wide with, in its center, the circle of the ecliptic which defines the apparent course of the Sun around the Earth (the ecliptic — and therefore the zodiac, is nothing but the tilt of the Earth in its orbit and therefore, by definition, the Sun has an ecliptic latitude of 0°). This zodiacal band has nothing to do with the groupings of stars (the constellations) that can be observed, from the Earth, in its background, and should therefore not be confused with the constellations zodiac which is only the stellar decor on the background of which the zodiacal cycles of the Sun, the Moon and the planets take place.
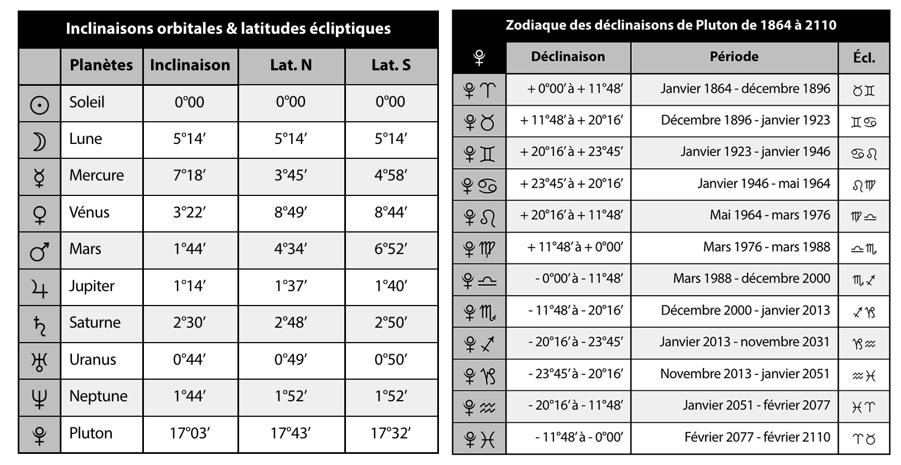
No planet faithfully follows the course of the Sun on the ecliptic: their orbits are all more or less inclined with respect to this plane (left table above), and their ecliptic latitudes (heights north or south in relation to this plane) vary according to the periodic oscillation of their orbit, which affects their declinations: each planet thus has its own zodiac, different from the solar zodiac.
It is the orbit of Pluto which has the strongest inclination (more or less 17°) on the ecliptic. When he is at his ecliptic latitude Maximum North or South, it is located outside the zodiacal band of 8.5° which contains approximately the apparent trajectories of all the planets which were known in antiquity.
The plane of Pluto’s orbit intersects that of the ecliptic in the axis of 20° Cancer-Capricorn, the declination of Pluto will only be substantially identical to that of the Sun around these positions. Pluto’s orbit is at its maximum in North declination around 20° Scorpio and in South declination around 20° Taurus. However, the ephemeris, which astrologers use to calculate the charts, only consider the projection of the positions of Pluto on the plane of the ecliptic, without taking into account its real declinations. Therefore the positions of Pluto in Signs given by the ephemerides are false.
The table on the right above shows the actual positions of Pluto in Signs for its entire current cycle, from 1864 to 2110. We can see that Pluto takes much longer to travel through its Taurus positions (27 years) than its Scorpio positions. (13 years). This is explained by the fact that Pluto is at its aphelion (point of its trajectory farthest from the Sun) in Taurus: it is therefore much slower than when it is at its perihelion (point of its trajectory closest to the Sun) in Scorpio.
The table below represents the sinusoids of the declinations of the Sun (ecliptic, in orange) and Pluto (in black). The Zodiac Signs below are defined by the positions of the Sun on the ecliptic. The black circles on the sinusoid of Pluto represent the real positions in Signs of this planet.
▶ Example: the Sun’s declination of 0° on the equator (beginning of the orange sinusoid of the ecliptic on the left) corresponds to 0° Aries. The dashed lines parallel to the equator correspond to the declinations which define the limits between the Sun Signs. If we project the position of Pluto on the ecliptic as the astrological ephemerides do, it is effectively at 0° Aries. But in reality its declination is −14° 56′ South, which corresponds to a position of the Sun in Aquarius. While the declinations of the Sun in Aries on the ecliptic will increase in the northern hemisphere up to 11.48° (beginning of Taurus), those of Pluto will increase in the southern hemisphere, going from Aquarius-like declinations to Pisces type. This means that a Pluto located at the beginning of Aries in the ephemeris is actually to be interpreted as a Pluto in Aquarius, and as a Pluto in Pisces if it is in the second half of Aries…
Due to the inclination of the plane of their respective geocentric orbits on that of the celestial equator, during their course around the Earth (apparent for the Sun and the planets, real for the Moon) the stars of the solar system cross the plane equatorial at 0° Aries (point which determines the vernal equinox), rise in the northern hemisphere where they culminate at the height of the Tropic of Cancer, then descend in the same hemisphere to cross the equator again at 0° Libra (point which determines the autumnal equinox) before starting their descent in the southern hemisphere until the height of the tropic of Capricorn, after which they go up in direction of the equator. These heights of a Planet in relation to the celestial equator are called the declinations.
In the diagrams below, the declinations and their corresponding zodiac signs are represented. The diurnal/nocturnal durations shown for each of the Signs have been calculated for 45° north latitude. To learn more about the astronomical zodiac, refer to this section.
The declination zodiac is universal: whatever the terrestrial latitude, it remains identical. If we accept the arbitrariness of the division of the ecliptic into twelve sectors of equal extents called “Signs”, each of them is characterized precisely by the arc of declination which it traverses (for example, from 0° to + 11° 34′ for Aries, etc.).
This universal zodiac manifests in the form of different photoperiodic zodiacs (of photo, light) specific to the different terrestrial latitudes and assigning to each Sign a specific ratio of increasing and decreasing daytime/nighttime durations. The diagram opposite illustrates this transition from declinations to photoperiods for a terrestrial latitude North of 45°.
In a geocentric frame of reference, the perihelion is transformed into perigee (the Sun is at perigee around the 1st January) and aphelion in apogee (for the sun, around the 1st July); the apogee-perigee axis is called axis of the apses. Due to the apparent elliptical course of the Sun on the ecliptic, the true seasons have unequal durations: spring (92 d 20 h in the northern hemisphere) and summer (93 d 15 h) are longer than autumn (89 d 15 h) and winter (89 d).
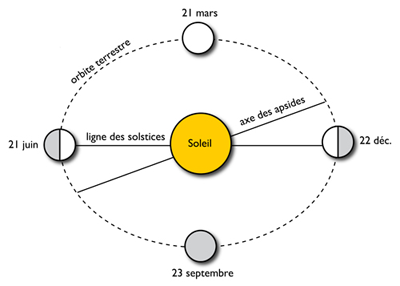Apses: We call apses the points on the orbit of a celestial body where it is nearest or furthest from the object around which it is rotating. In the case of the bodies of our solar system in orbit around the Sun, we use the terms aphelion and perihelion and, with respect to the lunar orbit (or indeed from a geocentric point of view in general), expressions apogee and perigee. The line of the apses connects these two points and therefore corresponds to the major axis of the elliptical orbits.
In spring and summer, the Sun moves away from the Earth (the true days lengthen, independently of the variations in declination, but at the same time the effects combine), in autumn and winter, the Sun approaches the Earth (true days are getting shorter). It goes without saying that variations in declination combined with seasonal effects are noticeable. At the equator, they are almost insensitive. What we call seasons therefore depends on three distinct but interdependent factors: 1) the inclination of the Earth in its orbit (N or S declination); 2) terrestrial latitude (climatological seasons); 3) and the position of the Sun in relation to the apses.
The zodiac is therefore “seasonal” than for the Sun. The Moon and the planets have their own declination zodiacs, independent of that of the Sun, which does not exclude a original approach to seasonal rhythms in chronopsychology.
▶ The stance circles: passing through the poles of the celestial sphere or the local sphere by intercepting the center of a star, they are used to define the position of this star. In the celestial sphere they are called hour circles, and are used to define to what “hour” is a star in relation to an arbitrary but common reference. Useful for sailors of yesteryear and shipwrecked astronomers of today. Note that the reference is the passage of the Sun at the gamma point: it is 0 h 00 sidereal, and the hour angle of the Sun is zero at noon in mean solar time. One hour later, the hour angle has varied by 15° (360/24) and it is 1 h 00 sidereal, and 13 h 00 in true solar time.
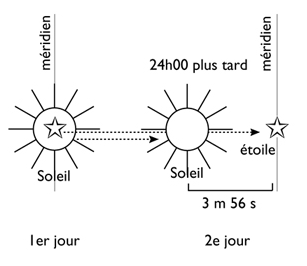
▶ right ascension: the right ascension of a star is the angle of the hour circle of the star and the hour circle of the gamma point. For the Sun, it is measured at the moment of the upper culmination of the mean Sun. More generally, the right ascension of a star measures the angle of the hour circle of the star and the hour circle given by the vernal point. The sidereal time of birth is nothing but the right ascension of the Midheaven: between the hour circle of the degree of the ecliptic at MC and the hour circle of the vernal point there is always an angle between 0 and 360°, which corresponds to the sidereal time elapsed since the passage to the meridian of the gamma point. The right ascension of the MC (ARMC) indicates the sidereal time of birth (T.S.N.). It is noted at one point that the Sun and a star “fixed” are in the same direction: this is the conventional origin of the sidereal day. In a second step, we note at what moment the star “fixed” is found in exactly the same place; we then notice that it takes 23 h 56 m 04 s for the Earth to make a complete turn on itself.
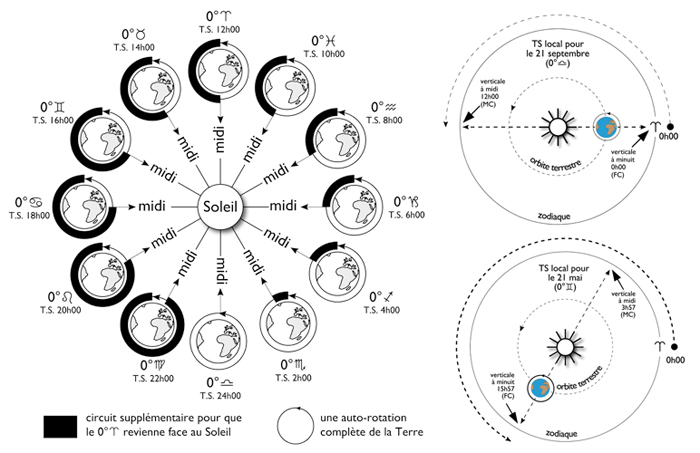
The solar day: It measures two consecutive passages of the Sun in relation to the same place of terrestrial observation, i.e. in relation to the meridian. The solar day “is” 24 h 00, and is also called “true day”. The true noon therefore measures 2 consecutive passages of the Sun at the meridian of the observatory, when the Sun is at the height of its daily course. The solar day is therefore 3m56s longer than the sidereal day: everything depends on the points of reference that we give ourselves to measure the flow of Time.
Average day: It is completely artificial and conventional. Also named calendar day, it allows us to divide sidereal time into equal slices… to the delight of watchmaking mechanics.
The orbit of the Earth being elliptical, the distance of our planet from the Sun knows a minima (perihelion, at 147 million km) and a maximum (aphelion, at 152 million km). Its orbital speed therefore accelerates (from maxima to minima) then decelerates (from minima to maxima); it follows that the length of the solar day varies according to the distance from the Earth to the Sun; the length of the solar day also varies due to the fact that the Earth is tilted by 23° 27′ with respect to the solar equatorial plane (variations in declination). the movement is therefore faster towards the perihelion and slower towards the aphelion, and affects the length of the true day. The interaction between these two phenomena, hopeless for the immutable regularity of calendar and watchmaking mechanics, led to the creation of a mean solar day, immutable and normative (‘R’ level). The difference between mean day and solar day is called equation of time.
Solar time and mean time coincide during the passage of the Earth at perihelion (1st January), at aphelion (1st July) (semi-major axis of the ellipse of Earth’s orbit), and when the Earth crosses one of the minor axes of the ellipse (in April and September), the irregularity of these periodicities resulting from the accelerations- decelerations of the Earth in its orbit. Outside these dates (also average), the average time can be ahead of solar time (until +16 min at the end of October) or late (up to −14 min in mid-February).
Our ephemerides being calculated in mean time, the Sun is not always at MC when it is true noon at the local meridian. On 11th February, for example, for the Greenwich observatory, the Sun is, at noon, at 3° 30′ Before the MC. At a rate of 4 min per degree, it “lack” well 14 m. On 28th October, this same mean Sun is at 4° 00′ after the MC. He is this time ahead of ahead of 16 min. On the other hand, the Sun is indeed exactly at the MC around the dates indicated above (which are, let us remember, average dates). Note that the equation of time is of little importance, since both the Civil Registry and the ephemerides use the same average time frame of reference.
On the other hand, it will be better understood that the Tables of the Houses are based on the right ascension of the MC (AR/MC), see below), only tell us about the relative position of the Sun in the local sphere. The other planets also have their little fantasies (eccentricity of the ellipse, ecliptic latitude), in no way identifiable with those of the Sun. At the limit, to have a representation close to reality of the situation of the planets in the local sphere, it would be necessary as many House tables as there are planets.
▶ Zodiac Signs & constellations: videos
▶ Astronomie des Maisons
▶ Introduction à la cosmogonie astrologique
▶ Astronomy of planets
▶ Thème de domitude et hiérarchisation planétaire
▶ The zodiac and the precession of the equinoxes
▶ The astronomical reality of the zodiac
▶ The human reflexology zodiac
Les significations planétaires
par
620 pages. Illustrations en couleur.
La décision de ne traiter dans ce livre que des significations planétaires ne repose pas sur une sous-estimation du rôle des Signes du zodiaque et des Maisons. Le traditionnel trio Planètes-Zodiaque-Maisons est en effet l’expression d’une structure qui classe ces trois plans selon leur ordre de préséance et dans ce triptyque hiérarchisé, les Planètes occupent le premier rang.
La première partie de ce livre rassemble donc, sous une forme abondamment illustrée de schémas pédagogiques et tableaux explicatifs, une édition originale revue, augmentée et actualisée des textes consacrés aux significations planétaires telles qu’elles ont été définies par l’astrologie conditionaliste et une présentation détaillée des méthodes de hiérarchisation planétaire et d’interprétation accompagnées de nombreux exemples concrets illustrés par des Thèmes de célébrités.
La deuxième partie est consacrée, d’une part à une présentation critique des fondements traditionnels des significations planétaires, d’autre part à une présentation des rapports entre signaux et symboles, astrologie et psychologie. Enfin, la troisième partie présente brièvement les racines astrométriques des significations planétaires… et propose une voie de sortie de l’astrologie pour accéder à une plus vaste dimension noologique et spirituelle qui la prolonge et la contient.
Téléchargez-le dès maintenant dans notre boutique
Pluton planète naine : une erreur géante
par
117 pages. Illustrations en couleur.
Pluton ne fait plus partie des planètes majeures de notre système solaire : telle est la décision prise par une infime minorité d’astronomes lors de l’Assemblée Générale de l’Union Astronomique Internationale qui s’est tenue à Prague en août 2006. Elle est reléguée au rang de “planète naine”, au même titre que les nombreux astres découverts au-delà de son orbite.
Ce livre récapitule et analyse en détail le pourquoi et le comment de cette incroyable et irrationnelle décision contestée par de très nombreux astronomes de premier plan. Quelles sont les effets de cette “nanification” de Pluton sur son statut astrologique ? Faut-il remettre en question son influence et ses significations astro-psychologiques qui semblaient avérées depuis sa découverte en 1930 ? Les “plutoniens” ont-ils cessé d’exister depuis cette décision charlatanesque ? Ce livre pose également le problème des astres transplutoniens nouvellement découverts. Quel statut astrologique et quelles influences et significations précises leur accorder ?
Enfin, cet ouvrage propose une vision unitaire du système solaire qui démontre, chiffes et arguments rationnels à l’appui, que Pluton en est toujours un élément essentiel, ce qui est loin d’être le cas pour les autres astres au-delà de son orbite. Après avoir lu ce livre, vous saurez quoi répondre à ceux qui pensent avoir trouvé, avec l’exclusion de Pluton du cortège planétaire traditionnel, un nouvel argument contre l’astrologie !
Téléchargez-le dès maintenant dans notre boutique
