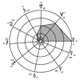
Organisation des demi-grands axes des orbites principales
Les distances moyennes au Soleil ou demi-grands axes varient, pour nos neuf planètes connues, de 0,387 UA (Mercure) à 39,44 UA (Pluton). En raison de leur excentricité, Mercure se rapproche du Soleil jusqu’à 0,31 UA, Pluton s’en éloigne jusqu’à 49 UA. Kepler a tenté d’intégrer dans des polyèdres emboîtés toutes les variations de distances (voir tableau des données) des planètes connues à son époque. Dans sa vision de l’Harmonie du Monde, fondée sur la géométrie et les nombres simples, chaque orbite devait générer la suivante. Après Kepler, au XVIIIe siècle, les astronomes allemands Wolf, puis Titius (1729–1796) et Bode (1747–1826) ont lié une part de leur postérité à la progression géométrique donnant, avec une “bonne incertitude de l’ordre de 5 %” [1], les distances (Dn) héliocentriques :

Dans la puissance n-ième de 2, n prend la valeur de −∞ pour Mercure, 0 pour Vénus, 1 pour Terre, 2 pour Mars, 3 pour une orbite sans planète connue au moment où la formule était posée ; et l’on progresse en ajoutant une unité. À partir de Neptune (n = 7) la “bonne incertitude” passe de 5 % a 22 %. À 49 % dans le cas de Pluton (n = 8)… ce qui est plutôt décourageant pour les nombres suivants. La formule doit d’être citée, non pas à sa rigueur, mais à son succès historique : pour n = 3, qui entraîne 0,4 + 0,3 × 8 = 2,8… on ne connaissait aucune planète.
Giuseppe Piazzi (1746–1826), astronome italien, mit fin à cette anomalie en découvrant, le 1er janvier 1801, le plus gros des astéroïdes qu’il s’empressa de nommer Cérès, en hommage à l’ancienne déesse de la Sicile (ce qui devrait ressortir dans ses significations) et aussi “Ferdinandea” en l’honneur de Ferdinand I, roi des Deux-Siciles. Pourtant, comme pourraient l’observer Evry Schatzman ou Jean-Claude Pecker, il faut beaucoup d’imagination pour voir une déesse et un roi dans un caillou de 1 000 km de diamètre, même s’il est riche en carbone et silicates hydratés ! Depuis G. Piazzi, plus de 3 500 astéroïdes ont été répertoriés. On a renoncé à leur donner des noms mythiques ou princiers. Ils portent des numéros… Ressembleraient-ils à des bagnards, des assujettis à la Sécurité Sociale ?
Si la distance héliocentrique de 2,8 UA participe à la cohérence du système solaire, en l’absence de critères de sélection comme pourraient l’être le diamètre de la planète ou son excentricité, elle n’a pas de représentant exclusif. Avec une incertitude de 2 % les candidats se multiplient : Pallas (2,77), Laetitia (2,77), Éléonore (2,79), Kepler (2,68), Dembowska (2,92), Eunomia (2,64). L’utilisation des cycles correspondants ne permet pas des analyses contrôlables. À quel astricule revient le mérite de conduire la maturation à l’âge jupitérien ? À Cérès, Cybèle, Pallas, ou au matricule 1668 (2,8 UA) ? L’hypothèse d’un effet global, guère mesurable, va à l’encontre du principe de fonctions différenciées qui, pour des raisons encore indémontrées impose un seul astre par fonction… Notre Soleil serait-il en “représentation de Représentation” (voir 2e partie) s’il n’était seul ? Peut-être, mais un peu moins. Ainsi, en astrologie, les éléments célestes multiples, astéroïdes, parts, aspects mineurs, foyers vides, rejoignent une fonction contraire au Soleil dans leurs significations. Pluton, probablement parce qu’il contribue à l’harmonie du système solaire, reste le représentant décisif, non pas exclusif, de la pluralité.
La découverte d’Uranus (1781) par W. Herschel (1738–1822) a assuré le deuxième exploit historique de la loi Titius-Bode, la distance moyenne d’Uranus, à 19,2 UA, confirmant le rang n = 6, par un beau résultat de 19,6 UA. Lorsque Urbain Le Verrier (1811–1877) a calculé les éléments de la “troublante” d’Uranus, c’est-à-dire Neptune, pour le demi-grand axe, il a tout simplement adopté un nombre proche du double d’Uranus, en proposant 36,15 UA alors que Neptune est à 30,109 UA. En dehors de la longitude, ses résultats sur la masse, l’excentricité, la durée de révolution sidérale, la longitude du périhélie, étaient grossièrement erronés. “Il y eut une sorte de désappointement lorsqu’on connut (septembre 1846) l’orbite de la planète nouvelle…” [2].
Mais la science méthodique, de méthode Coué, reprend vite son souffle. Vous trouverez difficilement l’inventaire de ses miracles truqués dans sa librairie spécialisée, aussi difficilement que le nom des astrologues dans ses dictionnaires. Qu’est-ce que l’intégrisme rationaliste au juste ? Une forme de liberté de censure ?
Malgré ses mémorables réussites, la formule Titius-Bode divise les astronomes de notre temps. Tous n’y croient pas. Les réticents pourraient avancer que dans un monde de gravitation régit par une loi en inverse carré (1 / R2) il est gênant d’avoir comme loi des orbites une progression géométrique (C + k × An), Quel pont jeter entre une loi numérique différente de la loi physique qu’elle prétend contenir ? Evry Schatzman, astronome et astrophysicien, a vu ou flairé le piège. Dans son livre didactique Les Planètes naissent aussi [3], il préfère reprendre, sans le citer, une thèse d’O. Schmidt, physicien soviétique, qui sépare distinctement les planètes rapides (de Mercure à Mars) des planètes lentes (Jupiter à Pluton), comme le font les astrologues sans avoir lu ses Quatre Leçons sur la théorie de l’origine de la Terre [4]. L’hétérogénéité des densités justifiant la distinction, car les planètes proches sont denses, les lointaines le sont moins, E. Schatzman, et O. Schmidt, qui a l’autorité du découvreur, font état de deux progressions de racines carrées avec des constantes différentes. Deux équations de droites qu’O. Schmidt commente ainsi :

“autrement dit, les racines carrées des distances des planètes au Soleil forment une progression arithmétique. C’est l’énoncé le plus simple de la loi des distances planétaires.
En déterminant les coefficients a et b séparément pour chacun des deux groupes de planètes […], nous obtenons les tableaux suivants (en prenant pour unité l’unité astronomique, c’est-à-dire la distance moyenne de la Terre au Soleil).”
Pour le groupe des planètes éloignées :
| Planètes |
Jupiter |
Saturne |
Uranus |
Neptune |
Pluton |
| √Rn théorique |
2,28 |
3,38 |
4,28 |
5,23 |
6,28 |
| √Rn réelle |
2,28 |
3,09 |
4,38 |
5,48 |
6,29 |
et pour le groupe des planètes proches :
| Planètes |
Mercure |
Vénus |
Terre |
Mars |
| √Rn théorique |
0,62 |
0,82 |
1,02 |
1,22 |
| √Rn réelle |
0,62 |
0,85 |
1 |
1,23 |
“La différence entre l’observation et la représentation est très petite…” conclut E. Schatzman. Elle l’est, si l’on calcule le pourcentage d’erreur sur la racine carrée de la distance. L’erreur devient grossière lorsqu’on retourne à ce que l’on propose de mesurer : les distances et non leurs racines. 8 % d’erreur sur Vénus, 20 % sur Saturne, 5 % sur Uranus, 10 % sur Neptune… mais le Président de l’Union Rationaliste est satisfait : “… cette représentation est la meilleure des représentations que l’on puisse trouver de la distance des planètes.” Devant tant de bonheur, on ne peut que mieux savourer l’humour et la déliquescence de ses péroraisons anti-astrologiques dans les Cahiers Rationalistes (n° 335) : “Mais alors, messieurs et mesdames les astrologues, ne nous importunez pas de vos prétentions scientifiques, laissez au vestiaire le beau vocabulaire, les mots dont vous ignorez le sens.” Rationaliste ? Un beau mot que l’on peut laisser au vestiaire pour de plus raisonnables prétentions.
| |
5 |
6 |
l |
7 |
w |
8 |
0 |
- |
= |
; |
| n |
−∞ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 0,4 + 0,3 × 2n |
0,4 |
0,7 |
1 |
1,6 |
2,8 |
5,2 |
10 |
19,6 |
38,8 |
77,2 |
| Demi-grand axe |
0,38 |
0,72 |
1 |
1,52 |
2,8 |
5,2 |
9,55 |
19,2 |
30,1 |
39,4 |
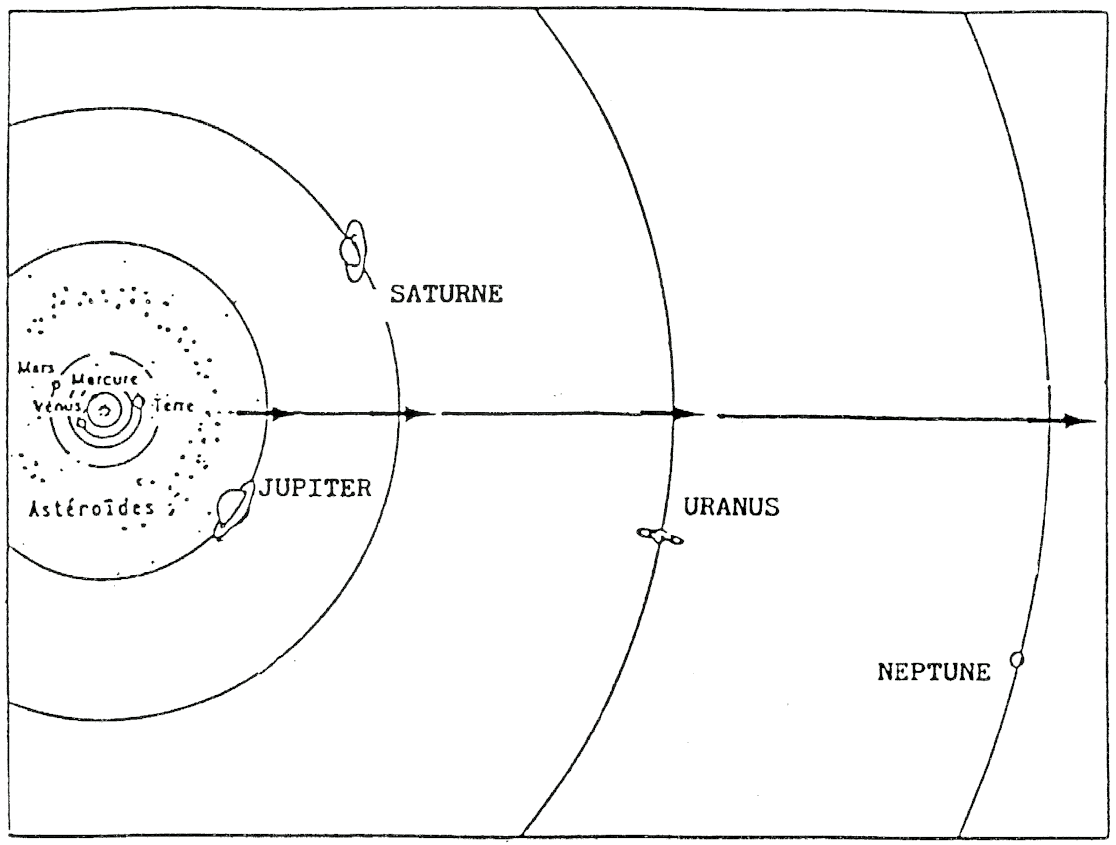
FIG. 1 — Loi de Titius-Bode (Demi-grand axe ≈ 0,4 + 0,3 × 2n).
L’espace-temps est courbe, la lumière s’infléchit près du Soleil, mais, inexorable, la loi de Titius-Bode va droit devant elle… pour rater sa cible à partir de Neptune et sortir du décor avec Pluton. Aucun engin cosmique ne suivrait pareille trajectoire.
Article suivant — 1.3. Courbure des interdistances & progression par les angles
[1] Le système solaire. Thérèse Encrenaz. Jean-Pierre Bibring. Éd. du CNRS, 1987.
[2] Cours d’astronomie. Hervé Faye. Gauthier-Villars, 1881.
[3] Les planètes naissent aussi. Evry Schatzman. Éd. Del Duca, 1960.
[4] Quatre leçons sur la théorie de l’origine de la Terre. O. Schmidt. Éd. de Moscou, 1959.