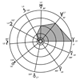
Organisation des demi-grands axes des orbites principales
S’il n’y avait que la géométrie sans la physique, l’axe de symétrie de la Fig. 5 se tracerait, en passant par le Soleil, de Pluton, 0°, à la longitude opposée, 180°. Les astéroïdes (184°) occupent cette position apparemment critique, et l’on peut chercher dans cet axe, non pas la symétrie du système, mais les raisons d’orbites mal conformées. Pluton et son compagnon Charon en font partie par leurs dimensions de gros satellites couplés, d’astres contestables. Mercure, un excentrique qui ne brille ni par la taille, ni par la masse, ne semble pas avoir apprécié la proximité du premier diamètre. On est conduit à placer ici la zone frontale du système solaire, telle que le suggère sa rencontre avec le vent interstellaire dans la direction de 18 h d’ascension droite et 30° Nord de déclinaison ; direction actuelle et approchée de l’apex. D’autres critères s’assureront du bien-fondé de cette hypothèse qui change la longitude 0° en repère extra-solaire plausible. Une indication à considérer, peut-être, sur les causes extérieures des caractéristiques du système solaire, d’une remarquable symétrie. Les angles et les lignes trigonométriques en dessinent la trace.
Les cotangentes (ou 1 / tangente) des élongations (valeurs angulaires de Ln) divisées par 2, conduisent aux formules génératrices des longitudes de référence et aux angles Â, B̂, Ĉ,… Dans la dernière colonne du tableau II, elles suffisent à représenter la division du système solaire en deux groupes :
▶ 0° à 180° (signe ‘+’ du cercle trigonométrique) : planètes massives, gazeuses, de faible densité, pourvues d’anneaux et de nombreux satellites… à l’exception des limites, Astéroïdes (184°) et Pluton (0°) qui pourraient former un groupe perturbé.
▶ 180° à 360° (signe ‘−’ du cercle trigonométrique) : planètes peu massives, denses, sans anneau, aucun ou peu de satellites.
Finalement, à 0° de position, dans la direction de Pluton, le Soleil, gazeux, peu dense, pourvu de satellites, appartient au groupe ‘+’.
Le classement ternaire, peu évident à l’observation, se justifie par :
▶ T : cotangente ‘+’ supérieure ou égale à 1.
▶ E : cotangente ‘+’ ou ‘−’ inférieure à 1.
▶ R : cotangente ‘−’ supérieure ou égale à 1.
En correspondance avec les constantes de nos planètes principales, ces définitions différencient l’espace selon nos modes de représentations formelles et selon les propriétés de l’espace. On retrouve, non pas le subjectif dans l’objectif des nouveaux croyants de la mystique physique mais l’objectif dans le subjectif des astrologues conditionalistes : les extrêmes du R.E.T. et le duo-duel du plan médian disposent de zones différentes dans un cercle d’un rayon a priori sans valeur absolue. Avec les tangentes, les extrêmes changent de signe, le plan médian reste composite, + et −. Ce n’est pas un signe de qualification d’influence positive ou négative, mais une information qui a été symbolisée sous une autre forme avant d’être explicitée sous celle-ci.
Toutes les lignes trigonométriques d’un angle  peuvent s’exprimer au moyen de la tangente du demi-angle,  / 2. S’il y a des corrélations à trouver entre les différentes longitudes du tableau II, les données à exploiter sont d’abord celles de la dernière colonne (cotangentes des demi-longitudes). Choisir entre tangentes et cotangentes paraît une affaire d’écriture puisque : cot = 1 / tan. Nous verrons que la physique introduit une importante différence.
Le tableau V couple les planètes dont la somme des rangs est égale à 9. On effectue la moyenne arithmétique des cotangentes en valeur absolue, ou leur différence algébrique divisée par 2. Le résultat, élevé au carré, est divisé par un coefficient empirique de 4,48 ou 2,11662.
Pour les couples intermédiaires d’ordre 1, 2, 3, en partant de Pluton 0, on approche, avec une incertitude inférieure à 1 %, du résultat de la formule :

dans laquelle :
- N = 1 : couple Neptune-Vénus.
- N = 2 : couple Uranus-Terre
- N = 3 : couple Saturne-Mars.
Les planètes aux positions limites, Pluton-Mercure, n’entrent pas dans cette formule transformable en :

conformément à l’équation littérale de l’hyperbole dont nous avons, pour les planètes, le cas particulier de valeurs discontinues et limitées par la condition : N < 4.

Les coniques se tiennent. Ceux qui préfèrent l’ellipse accorderont 0,529 au demi-petit axe, 1 au demi-grand axe. Pour les valeurs de x = 0,25, 0,5, 0,75, le rapport y / x correspond aux cotangentes des angles recherchés. L’ellipse, courbe fermée, rappelle les orbites planétaires et l’enveloppe de l’héliosphère, mais l’équation de l’hyperbole est plus directe. Leurs équations sont liées et concernent, entre autres phénomènes physiques, les figures d’interférences et de compositions de vibrations, pour les cas les plus simples.
Dans l’hyperbole de nos planètes idéales, on est tenté de prendre la cotangente de Jupiter (0,247), au lieu de 1/4, (0,25), comme constante. Il faut aussi observer que pour N = ∞, on déduit de l’équation 2) :

La valeur −0,280 correspond au rapport anharmonique des nombres 1, 4, 9, 16… obtenus par le rang (N) des couples 1, 2, 3, 4, élevés au carré. Selon une application de ce rapport désigné par (a, b, c, d) :

Avec : a = 1, b = 4, c = 9, d = 16 :


La mathématique enseigne qu’un nombre négatif n’a pas de racine, sauf s’il est imaginaire… mais plutôt que de nous lancer dans un exposé sur ces nombres qui n’ont rien à voir avec l’imagination, posons :

La valeur −0,52915 égale la tangente de 152,114°. Position L4 de Jupiter, et longitude moyenne des couples planétaires. Le coefficient 2,116, égal à 4 fois 0,52915 est donc en relation avec le rapport anharmonique des nombres 1, 4, 9, 16… et l’on peut en induire la tangente tan(L4) de Jupiter ou sa cotangente cot(L4 / 2).
TABLEAU V — Comparaison des données mesurées avec les données calculées pour les couples 1, 2, 3.
| Couple |
N |
n |
cot(Ln / 2) |
Demi-différence ΔN |
ΔN2 |
ΔN2
/ 4,48 |
YN
= 1/N2 − 1/16 |
Vénus
Neptune |
1
|
8
1 |
−1,926
+2,156 |
(2,156 + 1,926) / 2 =
2,041
|
4,166
|
0,930
|
0,9375
= 1/1 − 1/16 |
Terre
Uranus |
2
|
7
2 |
−0,821
+1,010 |
(1,010 + 0,821) / 2 =
0,916
|
0,838
|
0,187
|
0,1875
= 1/4 − 1/16 |
Mars
Saturne |
3
|
6
3 |
−0,342
+0,586 |
(0,586 + 0,342) / 2 =
0,464
|
0,216
|
0,048
|
0,0486
= 1/9 − 1/16 |
Cérès
Jupiter |
4
|
5
4 |
−0,038
+0,247 |
(0,247 + 0,038) / 2 =
0,143
|
0,02
|
1/220
|
1/240
= 1/15 − 1/16 |
D’une précision performante pour les couples 1, 2, 3, la formule est en défaut au couple N = 4… 15 n’étant ni le carré de 4, ni le carré d’un nombre entier. Il peut indiquer le début d’une suite de termes qui tendent vers 16, en rapport avec la pluralité des astéroïdes. La valeur absolue du demi-axe b (0,52915) de l’hyperbole renvoie néanmoins à la tangente tan(L4) de Jupiter… qui est une longitude moyenne, et dont on tire la cotangente cot(L4 / 2) de Jupiter, suivant la relation :

Sachant que cot(a) = 1 / 0,52915… on obtient, en résolvant l’équation : cot(a / 2) = 0,24827. a / 2 = 76,057°. D’où : L4 de Jupiter : 152,11°. Constante du système.
Selon ce qu’il tient à souligner, le mathématicien présente une formule sous l’angle propice à son idée (cf. les racines d’E. Schatzman). La mienne, après les nombres entiers, porterait sur la constante, autant que sur Jupiter. Si bien que j’écrirai :

Un bravo pour Jupiter qui, en tant qu’étoile manquée a failli prendre la place du Soleil. Aux lecteurs qui préfèrent les chiffres :

ou bien :

N désigne le rang des couples (1, 2, 3). La cotangente est celle de leur moyenne en valeur absolue ou de leur différence algébrique (colonne 3 du tableau V).

Après les différences, les sommes algébriques mettent les cotangentes en relation avec Jupiter et Mercure, et les entiers 4 et 5.
TABLEAU VI — Sommes algébriques des cotangentes pour les couples planétaires 1, 2, 3, 4.
| Couple |
N |
n |
cot(Ln / 2) |
Somme algébrique |
Vénus
Neptune |
1
|
8
1 |
−1,926
+2,156 |
2,156 − 1,926 = 0,23 |
Terre
Uranus |
2
|
7
2 |
−0,821
+1,010 |
1,010 − 0,821 = 0,189 |
Mars
Saturne |
3
|
6
3 |
−0,342
+0,586 |
0,586 − 0,342 = 0,244 |
Cérès
Jupiter |
4
|
5
4 |
−0,038
+0,247 |
0,247 − 0,038 = 0,209 |
Sensiblement, une alternance : 1/4, 1/5 … en observant que l’on peut également adopter la tangente tan(L9 / 2) de Mercure, soit, tan 168,71° = 0,1996, pour les couples pairs, la cotangente cot(L4 / 2) de Jupiter, soit cot(152,11° / 2) précédemment calculée : 0,2483. Les termes arrondis à 0,2 et 0,25 suffisent à la précision des résultats.
Des cotangentes calculées par la formule 2), les Ln / 2 de Mercure et Jupiter étant définies, découlent de nouvelles longitudes, de nouveaux angles de leurs différences, puis de nouveaux sinus et, enfin, une suite de distances d’un système solaire “moyenné”, rétabli dans sa symétrie.
TABLEAU VII — Longitudes et angles obtenus par la formule de calcul des cotangentes moyennes L−n / 2.
| Planète |
n |
cot(L−n / 2) |
L−n / 2 |
L−n |
Angle |
| Pluton |
0 |
|
0° |
0°,00 L−0 |
|
| Neptune |
1 |
+2,049 |
26°,01 |
52°,02 L−1 |
52°,02 Â− |
| Uranus |
2 |
+0,917 |
47°,50 |
95°,00 L−2 |
42°,98 B̂− |
| Saturne |
3 |
+0,467 |
64°,98 |
129°,96 L−3 |
34°,96 Ĉ− |
| Jupiter |
4 |
+0,148 |
81°,57 |
163°,13 L−4 |
33°,18 D̂− |
| Cérès |
5 |
−0,148 |
98°,43 |
196°,87 L−5 |
33°,73 Ê− |
| Mars |
6 |
−0,467 |
115°,02 |
230°,04 L−6 |
33°,18 F̂− |
| Terre |
7 |
−0,917 |
132°,5 |
265°,00 L−7 |
34°,96 Ĝ− |
| Vénus |
8 |
−2,049 |
153°,99 |
307°,98 L−8 |
42°,98 Ĥ− |
| Mercure |
9 |
−5,025 |
168°,75 |
337°,49 L−9 |
29°,51 Î− |
| Origine |
|
|
180° |
360° |
22°,51 Ĵ− |
TABLEAU VIII — Distances calculées (D−n) à partir de Pluton, en UA, par les produits successifs des sinus des angles Â−, B̂−, Ĉ−…
| Planète |
n |
Angle |
sinus |
D−n |
| Pluton |
0 |
|
|
39,44 |
| Neptune |
1 |
52°,02 Â− |
0,788 |
31,09 |
| Uranus |
2 |
42°,98 B̂− |
0,682 |
21,19 |
| Saturne |
3 |
34°,96 Ĉ− |
0,573 |
12,14 |
| Jupiter |
4 |
33°,18 D̂− |
0,547 |
6,65 |
| Cérès |
5 |
33°,73 Ê− |
0,555 |
3,69 |
| Mars |
6 |
33°,18 F̂− |
0,547 |
2,02 |
| Terre |
7 |
34°,96 Ĝ− |
0,573 |
1,16 |
| Vénus |
8 |
42°,98 Ĥ− |
0,682 |
0,79 |
| Mercure |
9 |
29°,51 Î− |
0,493 |
0,39 |
| α |
|
22°,51 Ĵ− |
0,383 |
0,15 |
En excluant Mercure pour respecter la symétrie des angles, la distance α devient égale à : 0,79 × sin 52,02° = 0,622.
Valeur proche de √0,387, demi-grand axe de Mercure. La constante des couples se calcule alors par :

Numériquement :

Dans le système solaire, au demi-grand axe de 4,95 UA correspond, pour l’astre sur cette orbite, une révolution sidérale de 11,01 ans, durée moyenne d’un cycle d’activité solaire. C’est aussi la distance de Jupiter au périhélie.
Si l’on répugne à exprimer cette durée en années, comme les auteurs de Recent Advances in Astrology [1], il suffit de changer les unités et d’adopter le coefficient de proportionnalité qui convient à la 3e loi de Kepler. Les mètres pour les distances, les secondes pour les durées donnent :

au lieu de

lorsqu’on adopte l’unité astronomique pour les distances et l’année pour unité de temps.
Cette corrélation entre le cycle moyen de l’activité solaire et une constante propre à tout le système met sur la voie des interactions Soleil-Planète, les cycles internes du Soleil se reflétant tant à la surface (taches, éruptions) que dans les régions externes, jusqu’aux limites de l’héliosphère. J’ai évoqué, d’autre part, une interaction extra-solaire, parce que la symétrie relative du système réel (Fig. 5) apparaît comme une déformation de celle (Fig. 7) que donneraient les distances dans un système moins sensible aux forces extérieures malgré sa cohérence interne.
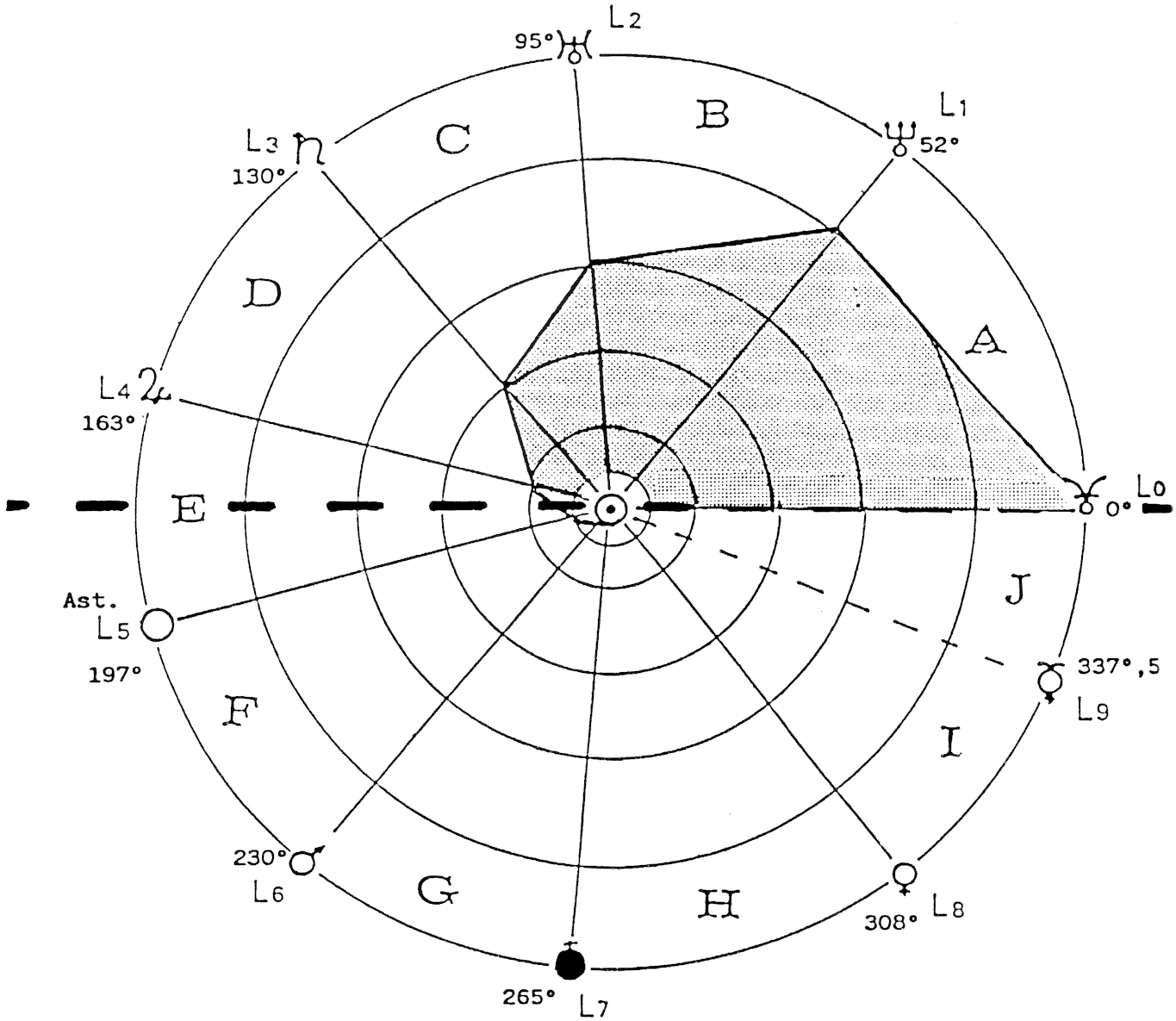
FIG. 7 — De la formule cot(L−N / 2) = 2,1166 ⋅ √(1 / N2 − 1 / 42), se déduisent les longitudes, les angles, les sinus, et de nouvelles distances. Dans ce système issu des données du système réel, le diamètre 0° - 180° devient un axe de symétrie en miroir qui, pour être parfait, renvoie Mercure à la longitude 360°, avec une distance arrivée de 0,622. L’intérêt de cette organisation du système solaire est autant dans cette symétrie que dans les nombres entiers qui y conduisent.
Article suivant — 1.5. Des entiers simples aux niveaux d’énergie
[1] Recent Advances in Natal Astrology. Compilé par Geoffrey Dean. Astrological Association, Décembre 1977.