The original notion of Aspect among the Babylonians

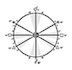
In the joint beginnings of astrology and astronomy a few millennia ago, Babylonian scholar-priests paid attention to only one Aspect: the conjunction (≈ 0°), major celestial phenomenon because the most visible. The astronomico-astrological tablets of the 18th to the 16th century BCE that have been found attest to this. This interest in conjunction alone seems to have lasted at least a thousand years, and it was only very gradually that the Aspect of opposition among Middle Eastern astrologers. To integrate it into knowledge, it was indeed necessary that the science of astronomical calculations had developed enough to make it possible to know and then predict when a planet above the horizon (therefore visible) formed an angle of ≈ 180° with a another under the horizon, therefore invisible. And it was only much later that the Aspects of quadrature (≈ 90°), of trine (≈ 120°) and sextile (≈ 60°).

The video below (4′ 27″) is a commented animation of the notion of Aspect among the Sumerians and Babylonians.

Classic Western Astrology, the result of the integration of this Babylonian knowledge and observations by Greek culture towards the 5th century BCE, is the heir to these discoveries and then to their progressive elaboration. Concerning the Aspects and their orbs, classical astrology called “traditional” does not have a theory to systematically explain their nature, number and operating principles.

The notion of Aspect according to Ptolemy in 2nd century

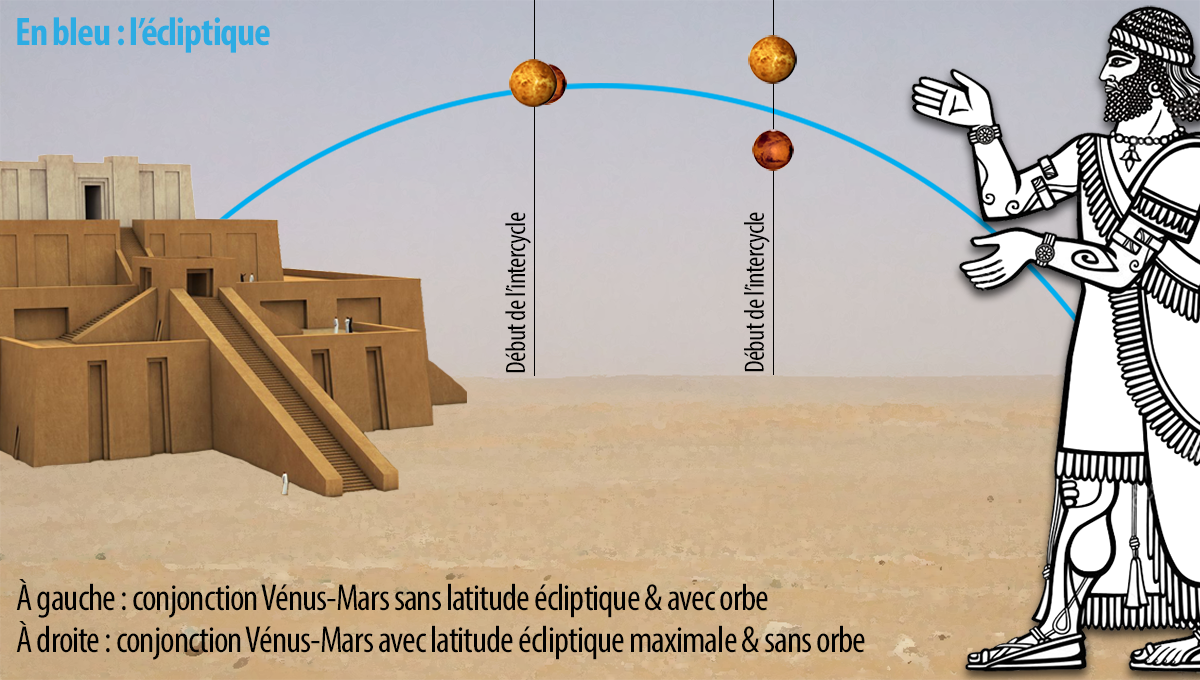
In his Tetrabiblos, written in 2nd century CE, the astronomer, astrologer, geographer and mathematician Claudius Ptolemy presents his own vision of astrology, but above all lists and presents encyclopaedically the astrological knowledge of his time as they were conceived by the Greco-Romans. This book is therefore a major historical reference, in that it testifies to the sources and foundations of the contemporary western astrology.

From a terminological point of view, it is remarkable to note that Ptolemy never uses the term “Aspect” in this book. It only devotes to what centuries later will be called the so-called Aspects “major” (conjunction, opposition, square, trine, sextile) than three paragraphs in the section titled The configurations of the zodiac signs of the chapter devoted to the zodiac. Here is the entirety of this text which is supposed to define what the Aspects are for almost two millennia:

“The first affinities which exist between the Signs of the zodiac are those which are produced by their reciprocal configurations. Are in mutual configuration: all the Signs which are in diametrically opposite positions and including two right angles, that is to say six Signs or 180°; those which are in a triangular position including a right angle plus a third of a right angle, that is to say four Signs or 120°; then those which are said to be square and which contain a right angle, that is to say three Signs or 90°; finally those which are in hexagonal position and which include two thirds of a right angle, that is to say two Signs or 60°.

Why have we traditionally accepted only these intervals? This will be easily understood with what follows. For the diametrical opposition, the explanation is obvious in itself, because the two zodiacal Signs meet on one and the same straight line. Then, if we take the two major fractions and superfractions that we find in music, and if we apply the fractions of 1/2 and 1/3 to the diametrical opposition made up of two right angles, we will obtain, with the first, the figure 1/2 of the square and with the second (1/3) the figure of the sextile and the trine. Superfractions, if we now apply the sesquialtery (3/2) and the sesquitierce (4/3) at the interval of 90° from a right angle, the sesquialtery will produce the figure of the square respectively at the sextile, and the sesquitierce the figure of the trine respectively at the square.

However, among these configurations, triangles and hexagons are called harmonics, because they are composed of Signs of the same gender, either entirely feminine or entirely masculine. But the squares and the diametrically disharmonic oppositions, because they constitute a relationship based on the opposition of Signs of the same kind.”

Still from the terminological point of view, note that the word “planet” does not appear in this description, whereas for a contemporary astrologer, the word “Aspect” is automatically associated with it. We must therefore face the facts: this text does not deal with Interplanetary aspects, but angular distances between zodiac signs. To avoid everything anachronism and risk of semantic confusion, so it’s best to assign different names to these two separate objects. We will therefore call here “zodiacal angles” the pseudo-Aspects defined by Ptolemy more than 1800 years ago, and we will reserve the name “Aspect” to the Interplanetary Aspects as they have been conceived since about the 17th century.

Right angles & musical intervals

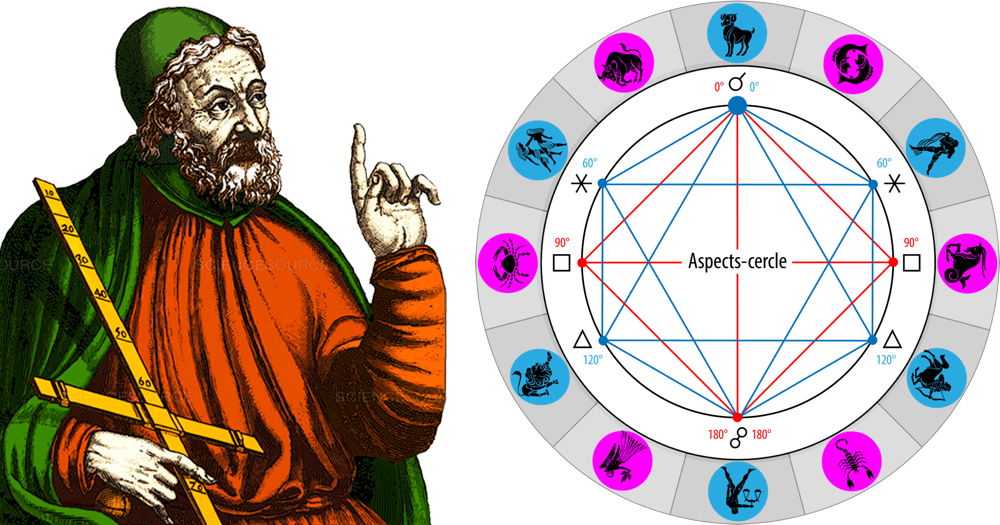
In his definition of zodiacal angles, Ptolemy refers both to the space (by geometry) and time (by music). The “right angles” belong to the repository spatial: these are the sides or vertices of regular polygons geometrically inscribed in the ecliptic circle of the zodiac. These figures belong to the elementary plane geometry of which Euclid systematically expounded the axiomatic around 300 BCE. The “intervals”, they come under the reference temporal: they refer to the Pythagorean arithmosophical theory according to which musical harmonies proceed from close relationship between notes and numbers, mathematical ratios resulting in frequencies. Indeed a sound is characterized by its frequency or the number of its vibrations per unit of time: the frequencies high are related to sounds treble, and the frequencies bass with the bass. In music, a interval thus defines the difference between two pitches of sound emitted simultaneously or successively.

This reference to musicology could have led him to give a dimension temporal (frequency, simultaneity, chronology) to his conception of the Aspects, and thus to leave the circle for the cycle. But Ptolemy did not, preferring geometricize musical intervals rather than viewing Aspects as time-bound phases like notes. In this he was faithful to the cultural heritage of Greek mathematicians, who placed geometry both at the heart and above all the sciences. But this blindness prevented him from developing a cyclical conception and therefore cinematic aspects. This temporal blindness also struck all those who referred to the Tetrabiblos for the next 18 centuries.

If he does not develop in the Tetrabiblos, astrological treatise, this correlation between zodiacal angles and musical intervals (therefore simultaneous or successive frequencies), he does so clearly in Book III of his work Harmonics, treatise on mathematical musicology in which he sets out the theories of the Pythagorean schools as well as the fruit of his own original research in this field.

You should know that for the ancient Greek scholars the soul or the structure of the world was essentially both geometric, mathematical and musical, music being considered the most perfect expression of cosmic harmony. The seven notes “natural” Western music are indeed related to the seven planets (this term including the Sun and the Moon) known in antiquity. Note in passing that Indian music, although very different, also uses seven basic notes called svaras. Since Plato, it had been considered that this septenary, after various astronomico-arithmosophical treatments according to their authors, formed by its numerical proportions a musical scale named “harmonia”, now referred to as “music of the spheres”.

Finally, let us specify that the thinkers of Greek Antiquity used a identical terminology for all of their disciplines, because of the analog thought system which then prevailed. It is therefore not surprising that Ptolemy was able to mix geometry, musicology, astronomy and astrology in this way.

What is surprising, on the other hand, is that Ptolemy focused on the zodiac rather than on planets to evoke the angles-intervals, whether in the Tetrabiblos or in the Harmonics. In this last work, the correlations between the planetary positions and the musical scale are nevertheless briefly exposed at the end of book III. He certainly mentions the angular distances between planets (so their “Aspects”), but he only defines them as zodiacal angles. And when he establishes direct analogical correspondences (without explicit reference to the zodiac therefore) between planets and musical frequencies, he does not refer to these angles calculated on the ecliptic and therefore in the celestial sphere, but, and very briefly, to planetary positions in the local sphere. Thus for him, the planets in the zone of their rising (Ascendant) and their setting (Descendant) are related to the low notes, and those in higher culmination (Midheaven) with the high notes. It doesn’t mention the Bottom-of-the-Sky, which is probably a very… serious oversight.

This analogy rests, if we transpose it to ranges of voices, on correspondences between the “head voice”, acute and therefore analogous to the planets also high in the sky and the “chest voice” (more or less low) and therefore analogous to planets close to the horizon or directly below. The sopranos and countertenors would thus be voices “Midheaven”, the mezzo-sopranos, baritones and tenors of voices “Ascendant” if they know how to go up in the treble or “Descendant” if they are more gifted to go down in the bass, and finally the contraltos and the bass of the voices “bottom-of-the-sky”.

The video below (6′ 32″) is a commented animation of the notion of Aspect in Ptolemy.

The zodiacal angles, pseudo-Aspects

Let us now return to Ptolemy’s reference text on the zodiacal angles which, as we will see, have only a very distant relationship with the contemporary notion of Aspect. To explain and justify its nature and characteristics, it certainly refers both to geometric space (the “right angles”) and time (the “intervals” musical which can be simultaneous or successive), but the space is clearly privileged since there is no question of kinematics: no movement such as the rotation of a planet is indicated, but all movement takes place in a temporality. The concept of “interval” thus seems here to have to be understood more in its mathematical definition of a set comprised between two values… which then makes it a Synonym of right angle.

The zodiac attributes in the Tetrabiblos are very different from those resulting from the introduction of the doctrine of the 4 Elements around the 16th century. The 12 Signs were classified by their gender alternatively “masculine” or “feminine” from Aries and by their seasonal position: “equinoctial” (Aries-Libra) and “solstitials” (Cancer-Capricorn) at the start of the season, “solid” in the middle of the season (Taurus-Leo-Scorpio-Aquarius) and “bicorporal” at the end of the season (Gemini-Virgo-Sagittarius-Pisces).

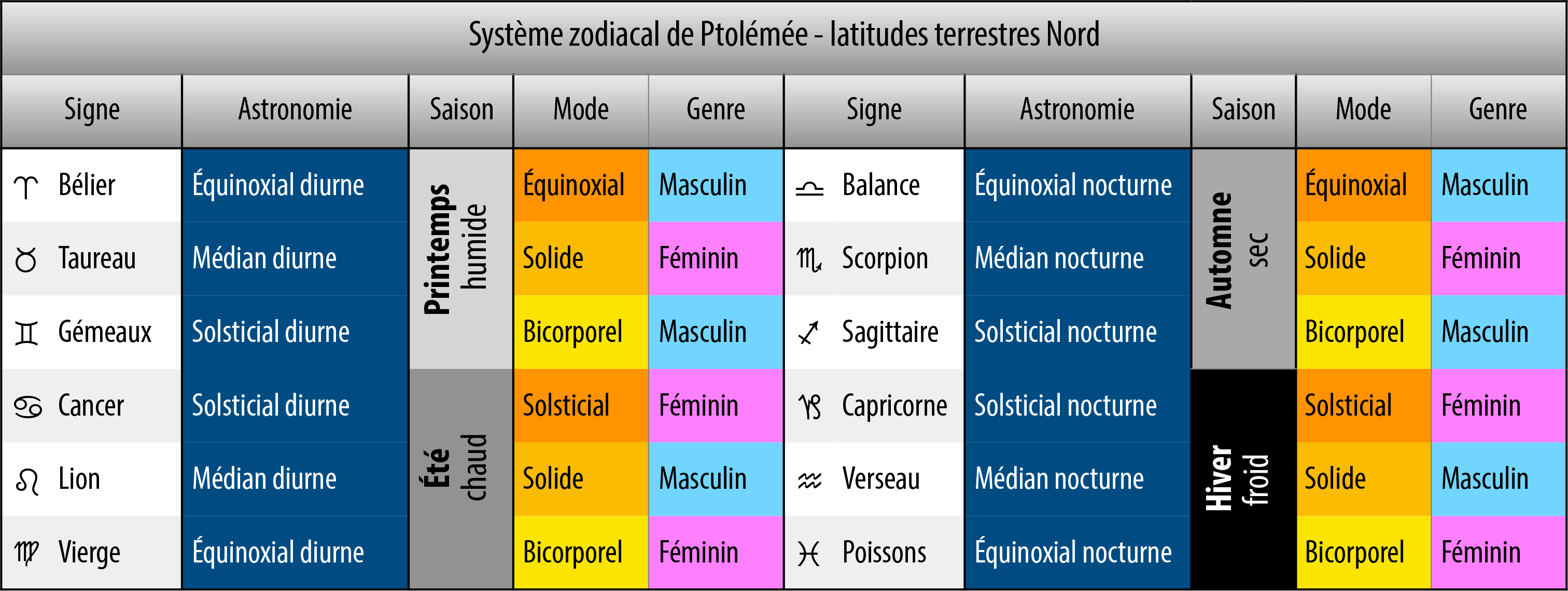
The zodiacal angles are “harmonics”, (trine, sextile) when they associate Signs of the same gender and “disharmonics” when they connect different kinds (square) or Signs of the same kind but diametrically opposed (opposition). The conjunction is not expressly mentioned, but given that according to these definitions it can only exist in the same Sign and that it is the inverse symmetry of the opposition, it is considered as “harmonic”.

The zodiacal angles major

The harmonic or disharmonic character of these zodiacal angles is determined by the regular polygons which can fit into the zodiacal circle and of which they are either the sides (sextile, square, trine) or the vertices (conjunction, opposition):

▶ Hexagon: polygon harmonic, it brings together the 6 Signs of the same male or female gender. The corresponding zodiacal angles are its sides, the sextiles (360/6 = 60°).
▶ Triangular: polygon harmonic, it brings together 3 Signs of the same kind, each occupying a different position in its season. The corresponding zodiacal angles are its sides, the trines (360/3 = 120°).
▶ Edge: polygon disharmonic, it brings together 4 Signs of opposite gender, each occupying the same position in its season. The corresponding zodiacal angles are its sides, the squares (360/4 = 90°).
▶ Conjunction-Opposition: the conjunction occurs in the same Sign; the opposition brings together 2 diametrically opposed Signs, therefore of the same kind. The corresponding zodiacal angles are the vertices of the square (360/1 = 0° or 360° and 360/2 = 180°).

These zodiacal angles based on fractions of whole numbers 1/1, 1/2, 1/3, 1/4 and 1/6 are at the origin of what will later be called the 5 Aspects called “major” (conjunction, opposition, trine, square, sextile). They are called “major” both because their effects are the strongest, and because they are the only ones that Ptolemy refers to, which distinguishes them from two Aspects “minors”, the semi-sextile (30°) and the quincunx (150°) which he mentions but does not name in the section entitled Unrelated Signs:

“The Signs of the zodiac which do not present any relation of affinity between them are called unrelated and strangers; […] they do not participate in any of the four configurations already mentioned, namely diametrical opposition, trine, square, sextile, but are distant from each other by one or five Signs. The Signs which are contiguous almost repel each other and, while being two, they embrace a single angle; those separated by five Signs divide the whole circle into unequal parts; and the other configurations produce an equal division of the circumference.”

This very short paragraph is of paramount importance in understanding the nature of the major zodiacal angles. These only exist within the framework of a static geometry and the binary division of the zodiac into Signs alternately “masculine” and “feminine” dictates to them possibility condition and at the same time imposes on them a major inconsistency. Let us specify here that in the Greek way of counting, the starting point is always included, which implies that two contiguous Signs are considered as “distant from each other by a Sign”.

The zodiacal angles minors, “unrelated and foreign”

This possibility condition is described in the last sentence: for a zodiac angle to be acceptable, it must be the product of a “equal division of the circumference”, otherwise the Signs it links are considered as “unrelated and foreign”. But Ptolemy himself departs from this rule in the case of the contiguous Signs.

1) The semi-sextile: contiguous Signs are indeed always of a different gender due to the masculine-feminine alternation which basically defines the Ptolemaic conception of the zodiac, and for this reason “almost repel each other”, which makes sense from the point of view of this gender theory. Ptolemy adds that “while being two, they embrace a unique angle”, which makes sense from a geometric point of view since, being contiguous, they effectively form a single angle.

But he is on the contrary totally illogical to eliminate the zodiacal angle that they form by invoking these two reasons while this angle of 30° does not derogate from the rule of “equal division of the circumference” since it is the side of a regular polygon, the dodecagon (360/12 = 30°). This angle, resulting from the division in two of the sextile, is harmonic, but it connects two Signs of opposite genders, so disharmonics. Ptolemy found himself there before a aporia: either the masculine and the feminine are not disharmonic, and in this case he can retain the harmonic semi-sextile of 30°, or they are disharmonic, and he must then eliminate this zodiac angle. He chose the second solution, which is to privilege the logic of zodiacal genders against that of regular polygons. This is the (un)reason for which the semi-sextile is absent from the list of these privileged zodiacal distances that are the “Aspects” Ptolemaic.

2) The quincunx: two Signs separated by a zodiacal distance of 150° are also considered “unrelated and foreign”. It is eg. the case of Aries and Virgo. Now these two Signs are of opposite gender: masculine for the first, feminine for the second, so disharmonics. But the angle of 150°, product of (360/2.4) does not make it possible to inscribe a regular polygon of which it would be one of the sides in the zodiacal circle. The quincunx was eliminated for this reason, whereas it belongs to the family of semi-sextiles (150/5 = 30°) and as such it would be a harmonic configuration… Here too Ptolemy was confronted with an aporia, but this time to resolve it, he chose to favor the criterion of “equal division of the circumference”, that is to say that of regular polygons. This is the (un)reason why the quincunx is absent from the list of these privileged zodiacal distances.

3) The semi-square: this zodiacal distance presented Ptolemy with another kind of logical problem, one so insoluble that he decided to do not mention, even implicitly, this 45° angle, product of the division in 2 of the square. The semi-square (360/8 = 45°) is indeed the side of a regular polygon, the octagon. As such, he should not have been excluded, but he was because of a major flaw: its 45° allow at a time a connection between harmonic signs (of the same gender, eg Aries & Gemini) and disharmonic signs (of opposite gender, eg Aries & Taurus). This is the (un)reason why the semi-square is absent from the list of these preferred zodiacal distances.

The eviction of the semi-sextile, the quincunx and the semi-square could have made a collateral logical victim, the opposition, if Ptolemy had been consistently faithful to one of his selection criteria for preferred zodiacal distances. The opposition, disharmonic angle belonging to the family of the square of which it is with the conjunction one of peaks, indeed connects two Signs of the same kind therefore harmonic. But in this case he wisely preferred break the gender rule… and too bad if the opposition, according to that of the zodiacal affinities, should have been considered as a harmonic angle!

As we see, the planets and their actual angular distances are totally absent from this nomenclature of preferred zodiacal distances. This absence cannot be the product of a ignoring: as an astronomer, Ptolemy perfectly knew how to measure and calculate these distances independently of the Signs. But as an astrologer, he felt obliged by tradition not to dissociate them from them. It is only in a later chapter of the Tetrabiblos, entitled The characteristics of the soul, that he engages in a systematic interpretation of interactions between pairs of planets known in his time.

Harmonies, disharmonies, benefits and malefices

He describes these relationships always using the equivalent terms of “benefic” or “harmonic” and “malefic” or “disharmonic”. These notions being identical to those he uses elsewhere to qualify the zodiacal angles, one might think that it then implicitly describes the effects of Interplanetary aspects, when this is not the case, even if these interpretations look like archaic versions of those that can usually be found in classical astrology manuals.

The character “benefic” or “malefic” of the “reports” between planets is determined, not by their Aspects in the present sense of this term, for which he substitutes the more vague term of “reports”, but by their “honorable position” or “dishonorable”. The criteria of honorability and its opposite are, according to Ptolemy, a complex, eclectic and confused mixture of parameters composed mainly of the positions of the planets in Signs and the zodiacal angles thus induced, Planetary rulerships, of direct or indirect movement (retrogradation), of the planetary presence in “key sectors” (AS-MC-DS-MC angles), as well as the eastern (ascending, from IC to MC) or western (descending, from MC to IC), diurnal or nocturnal (over or under the horizon) configuration.

In Ptolemy therefore, the notion of preferred zodiac angle replaces that of Interplanetary aspect. The fact that he describes these angles in terms of plane geometry shows that they are exclusively calculated in ecliptic longitudes. Finally, in such a system, a planet can be in a zodiac angle ratio with almost all the others since the notion of precise planetary angle is absent. In effect, regardless of their actual and precise angular distances, two planets are considered to be:

▶ In conjunction if they are in the same Sign, but not if they are in two adjacent Signs, therefore of different gender. Ex: two planets 29° apart in ecliptic longitude in Aries are “spouses”, whereas they are not if they are 2° apart but located astride the Male Aries and the female bull.
▶ In opposition if they are in two diametrically opposed Signs (180°), but not if these two Signs are not, which means that an angle of 182° between a planet at 29° Aries and another at 1° Scorpio n is not considered an opposition. They are therefore “unrelated” or “foreign” to each other (while they are in “zodiac quincunx”).
▶ In square if they are in two Signs 90° apart (e.g. Aries & Cancer), which means that a 59° angle between a planet at 1° Aries and another at 29° Leo is not considered a square, but as a trine.
▶ In sextile if they are in two Signs 60° apart (e.g. Aries & Gemini), which means that a 58° angle between a planet at 1° Aries and another at 29° Taurus is not considered a sextile.
▶ In trine if these Signs are separated by an angle of 120° (e.g. Aries & Leo), which means that an angle of 92° between a planet at 29° Aries and another at 1° Leo is considered a trine, but that the same angle of 92° between a planet at 29° Aries and another at 27° Leo is considered a square.

Orbs of 30°… or none

In such a system, the problem of orbs (number of degrees allowed before and after the exact Aspect for it to be considered effective) does not arise. Or more exactly, this orb is implicitly defined by the extent of a Sign, i.e. 360/12 = 30°. This means eg. that a planet in Aries, regardless of its precise position in that Sign, is automatically considered to be in zodiac angle 60° (value of a sextile Aspect) with another in Gemini or Aquarius, 90° (value of a square Aspect) with another in Cancer or Capricorn, 120° with another in Leo or in Sagittarius, (value of a trine Aspect), and finally 180° with another in Libra (value of an opposition Aspect).

Chart below is that of Arthur Rimbaud. The sky map of left represents the zodiacal angles privileged between masculine or feminine Signs, the one on the right Real aspects. It is observed that the opposition between the Sun in Libra and Pluto in Taurus at 6° 12′ of orb is not allowed there because these two Signs are not diametrically opposed. The sky map of right represents the Aspects. The Sun-Pluto opposition is admitted this time. We also observe that the right Chart, “non-Ptolemaic”, includes much less Aspects than the one on the left of zodiacal angles Ptolemaic.

An Astronomically Absurd Doctrine

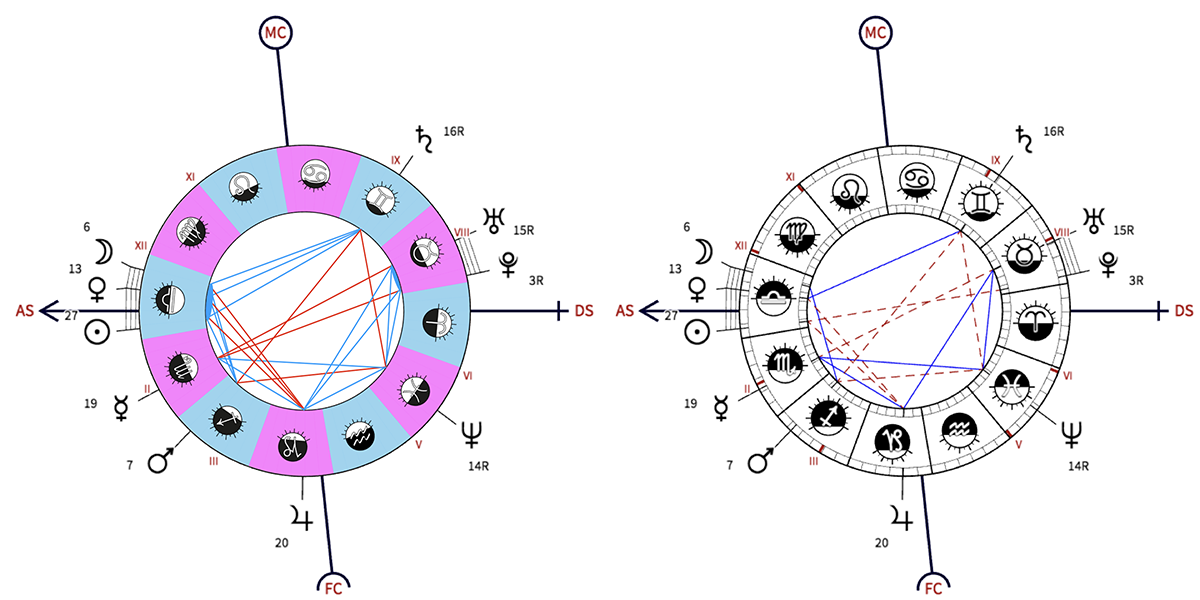
This astrological doctrine of zodiacal angles is absurd next to astronomical phenomena to which it is supposed to correspond: the actual angular distances between planets. Ptolemy, as astronomer as astrologer, could of course not ignore it. From the astronomical point of view, for example, he could only note and admit that two planets separated by 2° of ecliptic longitude are in conjunction orb, whatever the Signs in which they are located. He does so implicitly when he mentions the moon phases, so the Sun-Moon angular distances which can occur exactly at the boundary between two Signs. The Moon is indeed e.g. at its first or second quarter when it is 90° from the Sun, and not at any zodiacal angle between 60 and 120° determined by the Sun and Moon Signs. But on this subject (as on many others but not all) Ptolemy the astronomer disagrees with Ptolemy the astrologer.

The doctrine of zodiacal angles geometry explains why Ptolemy did not find it useful to formulate a system or theory of orbs. Indeed, by admitting these, the zodiacal angles privileged ones who take the place of Aspects in the Tetrabiblos would no longer form regular polygons in the native sky chart, which is a static representation, a frozen snapshot of the zodiaco-planetary positions for a given place and time. But the irregular polygons that these orbs were sure to form were considered to be imperfect forms by Greek geometry, therefore impossible for Ptolemy to accept.

But in his presentation of the techniques and forecasting methods like the planetary transits, he was indeed obliged to approach the notion of orb, without formulating it, referring to the motion of a planet before and after its exact zodiacal distance. During a Transit which can only be cinematic, the transiting planet is thus described as in “application” when it approaches the planet it will transit, and in “separation” when the transit has taken place and she is moving away from it. Application and separation imply the notion of orb: when does the application start (how many degrees back), when does the separation end (how many degrees forward)? To these questions Ptolemy does not answer.

On the other hand, it is in evoking transits that he makes two of the rare mentions of ecliptic latitudes contained in the Tetrabiblos. He indeed writes about the transiting planets that he is “convenient to observe their latitude to consider only the transits which take place on the same side of the ecliptic” that the transited planets, or again, in the chapter The duration of life, that “this harmful action [of the destructive planets] is also hindered if, both being celestial bodies, the meeting of the planet of the vital direction with the interfering planet does not occur at the same latitude.” But he does not give the reason for this recommendation, on which he does not insist.

This is where the design of the Aspects was more than 1800 years ago: they were not Interplanetary aspects, they were geometric shapes (a straight line, a square, four triangles and a hexagon), the sides or vertices of regular polygons drawn from any point of each Sign and determined by the ecliptic longitudes of these points and in a special case, the Transit, by the latitudes. The consonant or dissonant relationships of the Planets between themselves were only the consequences of those between the Signs they occupied, and the notion of ecliptic latitude in relation to such a conception of Native Sky Aspects of course didn’t any sense.

  Next article — The notion of Aspect from the 2nd to the 16th century